If the angles of a triangle are $${30^ \circ }$$ and $${45^ \circ }$$ and the included side is $$\left( {\sqrt 3 + 1} \right),$$   then what is the area of the tringle ?

Solution :

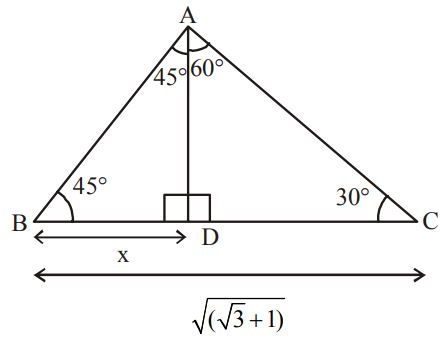
$$\eqalign{ & {\text{From, }}\Delta \,ADB,AD = BD = x \cr & {\text{In }}\Delta \,ADC, \cr & \tan {30^ \circ } = \frac{x}{{\sqrt 3 + 1 - x}} \cr & \Rightarrow \frac{1}{{\sqrt 3 }} = \frac{x}{{\sqrt 3 + 1 - x}} \cr & \Rightarrow \sqrt 3 \,x = \sqrt 3 + 1 - x \cr & \Rightarrow \left( {\sqrt 3 + 1} \right)x = \sqrt 3 + 1 \cr & x = \frac{{\sqrt 3 + 1}}{{\sqrt 3 + 1}} \cr & {\text{Area of }}\Delta \,ABC = \frac{1}{2} \times \left( {\sqrt 3 + 1} \right) \times 1 = \frac{{\sqrt 3 + 1}}{2} \cr} $$