Question
If tangents are drawn to the ellipse $${x^2} + 2{y^2} = 2,$$ then the locus of the mid-point of the intercept made by the tangents between the coordinate axes is-
A.
$$\frac{1}{{2{x^2}}} + \frac{1}{{4{y^2}}} = 1$$
B.
$$\frac{1}{{4{x^2}}} + \frac{1}{{2{y^2}}} = 1$$
C.
$$\frac{{{x^2}}}{2} + \frac{{{y^2}}}{4} = 1$$
D.
$$\frac{{{x^2}}}{4} + \frac{{{y^2}}}{2} = 1$$
Answer :
$$\frac{1}{{2{x^2}}} + \frac{1}{{4{y^2}}} = 1$$
Solution :
Any tangent to ellipse $$\frac{{{x^2}}}{2} + \frac{{{y^2}}}{1} = 1$$ is
$$\frac{{x\,\cos \,\theta }}{{\sqrt 2 }} + y\,\sin \,\theta = 1$$
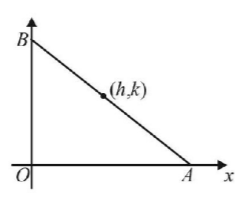
$$\eqalign{ & \therefore A\left( {\sqrt 2 \,\sec \,\theta ,\,0} \right)\,;\,B\left( {0,\,{\text{cosec}}\,\theta } \right) \cr & \Rightarrow 2h = \sqrt 2 \,\sec \,\theta \,\,{\text{and}}\,\,2k = {\text{cosec}}\,\theta \left( {{\text{using mid pt}}{\text{. formula}}} \right) \cr & \Rightarrow \cos \,\theta = \frac{1}{{\sqrt 2 \,h}}{\text{ and }}\sin \,\theta = \frac{1}{{2k}} \cr & \Rightarrow {\left( {\frac{1}{{\sqrt 2 \,h}}} \right)^2} + {\left( {\frac{1}{{2k}}} \right)^2} = 1 \cr & \Rightarrow \frac{1}{{2{h^2}}} + \frac{1}{{4{k^2}}} = 1 \cr} $$
Required locus,
$$\frac{1}{{2{x^2}}} + \frac{1}{{4{y^2}}} = 1$$
Any tangent to ellipse $$\frac{{{x^2}}}{2} + \frac{{{y^2}}}{1} = 1$$ is
$$\frac{{x\,\cos \,\theta }}{{\sqrt 2 }} + y\,\sin \,\theta = 1$$

$$\eqalign{ & \therefore A\left( {\sqrt 2 \,\sec \,\theta ,\,0} \right)\,;\,B\left( {0,\,{\text{cosec}}\,\theta } \right) \cr & \Rightarrow 2h = \sqrt 2 \,\sec \,\theta \,\,{\text{and}}\,\,2k = {\text{cosec}}\,\theta \left( {{\text{using mid pt}}{\text{. formula}}} \right) \cr & \Rightarrow \cos \,\theta = \frac{1}{{\sqrt 2 \,h}}{\text{ and }}\sin \,\theta = \frac{1}{{2k}} \cr & \Rightarrow {\left( {\frac{1}{{\sqrt 2 \,h}}} \right)^2} + {\left( {\frac{1}{{2k}}} \right)^2} = 1 \cr & \Rightarrow \frac{1}{{2{h^2}}} + \frac{1}{{4{k^2}}} = 1 \cr} $$
Required locus,
$$\frac{1}{{2{x^2}}} + \frac{1}{{4{y^2}}} = 1$$