Question
If tangents are drawn from any point on the line $$x + 4a = 0$$ to the parabola $${y^2} = 4ax,$$ then their chord of contact subtends angle at the vertex equal to :
A.
$$\frac{\pi }{4}$$
B.
$$\frac{\pi }{3}$$
C.
$$\frac{\pi }{2}$$
D.
$$\frac{\pi }{6}$$
Answer :
$$\frac{\pi }{2}$$
Solution :
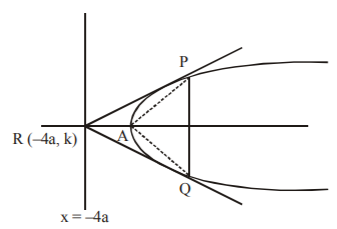
Let $$R\left( { - 4a,\,k} \right)$$ be any point on the line $$x = - 4a.$$ The equation of chord of contact $$PQ$$ w.r.t. $$P\left( { - 4a,\,k} \right)$$ is
$$y.k = 2a\left( {x - 4a} \right)......\left( 1 \right)$$
Making equation of parabola $${y^2} = 4ax$$ homogeneous using $$\left( 1 \right),$$ we get
$$\eqalign{ & {y^2} = 4ax\left( {\frac{{2ax - yk}}{{8{a^2}}}} \right) \cr & \Rightarrow 8{a^2}{x^2} - 8{a^2}{y^2} - 4akxy = 0 \cr} $$
This represents the pair of straight lines $$AP$$ and $$AQ.$$ Since coefficient of $${x^2} + $$ coefficient of $${y^2} = 0$$
$$\therefore \,\angle PAQ = {90^ \circ }$$ i.e. chord of contact $$PQ$$ subtends a right angle at the vertex.
Let $$R\left( { - 4a,\,k} \right)$$ be any point on the line $$x = - 4a.$$ The equation of chord of contact $$PQ$$ w.r.t. $$P\left( { - 4a,\,k} \right)$$ is

$$y.k = 2a\left( {x - 4a} \right)......\left( 1 \right)$$
Making equation of parabola $${y^2} = 4ax$$ homogeneous using $$\left( 1 \right),$$ we get
$$\eqalign{ & {y^2} = 4ax\left( {\frac{{2ax - yk}}{{8{a^2}}}} \right) \cr & \Rightarrow 8{a^2}{x^2} - 8{a^2}{y^2} - 4akxy = 0 \cr} $$
This represents the pair of straight lines $$AP$$ and $$AQ.$$ Since coefficient of $${x^2} + $$ coefficient of $${y^2} = 0$$
$$\therefore \,\angle PAQ = {90^ \circ }$$ i.e. chord of contact $$PQ$$ subtends a right angle at the vertex.