Question
If $$\sin {18^ \circ } = \frac{{\sqrt 5 - 1}}{4} ,$$ then what is the value of $$\sin {81^ \circ } ?$$
A.
$$\frac{{\sqrt {3 + \sqrt 5 } + \sqrt {5 - \sqrt 5 } }}{4}$$
B.
$$\frac{{\sqrt {3 + \sqrt 5 } + \sqrt {5 + \sqrt 5 } }}{4}$$
C.
$$\frac{{\sqrt {3 - \sqrt 5 } + \sqrt {5 - \sqrt 5 } }}{4}$$
D.
$$\frac{{\sqrt {3 + \sqrt 5 } - \sqrt {5 - \sqrt 5 } }}{4}$$
Answer :
$$\frac{{\sqrt {3 + \sqrt 5 } + \sqrt {5 - \sqrt 5 } }}{4}$$
Solution :
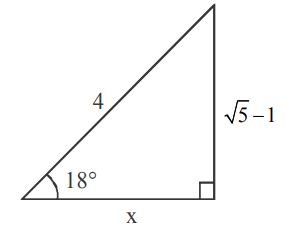
$$\eqalign{ & \because \sin {18^ \circ } = \frac{{\sqrt 5 - 1}}{4} \cr & {x^2} = {4^2} - {\left( {\sqrt 5 - 1} \right)^2} \cr & \Rightarrow x = \sqrt {10 + 2\sqrt 5 } \cr & \Rightarrow \cos {18^ \circ } = \frac{{\sqrt {10 + 2\sqrt 5 } }}{4} \cr & \Rightarrow 2{\cos ^2}9 - 1 = \frac{{\sqrt {10 + 2\sqrt 5 } }}{4} \cr & {\cos ^2}9 = \frac{{\sqrt {10 + 2\sqrt 5 } + 4}}{8} \cr & \Rightarrow \,{\sin ^2}81 = \frac{{4 + \sqrt {10 + 2\sqrt 5 } }}{8} \cr} $$
After squaring all the options available, we come to a conclusion that option $$\left( A \right)$$ is correct.

$$\eqalign{ & \because \sin {18^ \circ } = \frac{{\sqrt 5 - 1}}{4} \cr & {x^2} = {4^2} - {\left( {\sqrt 5 - 1} \right)^2} \cr & \Rightarrow x = \sqrt {10 + 2\sqrt 5 } \cr & \Rightarrow \cos {18^ \circ } = \frac{{\sqrt {10 + 2\sqrt 5 } }}{4} \cr & \Rightarrow 2{\cos ^2}9 - 1 = \frac{{\sqrt {10 + 2\sqrt 5 } }}{4} \cr & {\cos ^2}9 = \frac{{\sqrt {10 + 2\sqrt 5 } + 4}}{8} \cr & \Rightarrow \,{\sin ^2}81 = \frac{{4 + \sqrt {10 + 2\sqrt 5 } }}{8} \cr} $$
After squaring all the options available, we come to a conclusion that option $$\left( A \right)$$ is correct.