Question
If $$P\left( B \right) = \frac{3}{4},P\left( {A \cap B \cap \overline C } \right) = \frac{1}{3}$$ and $$P\left( {\overline A \cap B \cap \overline C } \right) = \frac{1}{3},$$ then $$P\left( {B \cap C} \right)$$ is
A.
$$\frac{1}{12}$$
B.
$$\frac{1}{6}$$
C.
$$\frac{1}{15}$$
D.
$$\frac{1}{9}$$
Answer :
$$\frac{1}{12}$$
Solution :
Given that $$P\left( B \right) = \frac{3}{4},P\left( {A \cap B \cap \overline C } \right) = \frac{1}{3}$$
$$P\left( {\overline A \cap B \cap \overline C } \right) = \frac{1}{3}$$
From venn diagram, we see
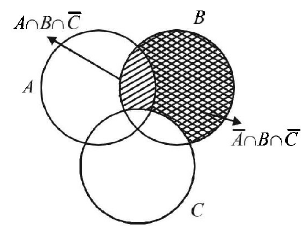
$$\eqalign{ & B \cap C \equiv B - \left( {A \cap B \cap \overline C } \right) - \left( {\overline A \cap B \cap \overline C } \right) \cr & \Rightarrow P\left( {B \cap C} \right) = P\left( B \right) - P\left( {A \cap B \cap \overline C } \right) - P\left( {\overline A \cap B \cap \overline C } \right) \cr & \Rightarrow \,\,P\left( {B \cap C} \right) = \frac{3}{4} - \frac{1}{3} - \frac{1}{3} \cr & = \frac{{9 - 4 - 4}}{{12}} \cr & = \frac{1}{{12}} \cr} $$
Given that $$P\left( B \right) = \frac{3}{4},P\left( {A \cap B \cap \overline C } \right) = \frac{1}{3}$$
$$P\left( {\overline A \cap B \cap \overline C } \right) = \frac{1}{3}$$
From venn diagram, we see

$$\eqalign{ & B \cap C \equiv B - \left( {A \cap B \cap \overline C } \right) - \left( {\overline A \cap B \cap \overline C } \right) \cr & \Rightarrow P\left( {B \cap C} \right) = P\left( B \right) - P\left( {A \cap B \cap \overline C } \right) - P\left( {\overline A \cap B \cap \overline C } \right) \cr & \Rightarrow \,\,P\left( {B \cap C} \right) = \frac{3}{4} - \frac{1}{3} - \frac{1}{3} \cr & = \frac{{9 - 4 - 4}}{{12}} \cr & = \frac{1}{{12}} \cr} $$