Question
If $${n_1},{n_2}$$ and $${n_3}$$ are the fundamental frequencies of three segments into which a string is divided, then the original fundamental frequency $$n$$ of the string is given by
A.
$$\frac{1}{n} = \frac{1}{{{n_1}}} + \frac{1}{{{n_2}}} + \frac{1}{{{n_3}}}$$
B.
$$\frac{1}{{\sqrt n }} = \frac{1}{{\sqrt {{n_1}} }} + \frac{1}{{\sqrt {{n_2}} }} + \frac{1}{{\sqrt {{n_3}} }}$$
C.
$$\sqrt n = \sqrt {{n_1}} + \sqrt {{n_2}} + \sqrt {{n_3}} $$
D.
$$n = {n_1} + {n_2} + {n_3}$$
Answer :
$$\frac{1}{n} = \frac{1}{{{n_1}}} + \frac{1}{{{n_2}}} + \frac{1}{{{n_3}}}$$
Solution :
In this problem, the fundamental frequencies of each part could be find. The fundamental frequency of the complete wire could be find. One should check each option for the given values.
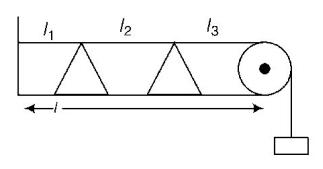
For Ist part, $${n_1} = \frac{v}{{2{l_1}}} \Rightarrow {l_1} = \frac{v}{{2{n_1}}}$$
For IInd part, $${n_2} = \frac{v}{{2{l_2}}} \Rightarrow {l_2} = \frac{v}{{2{n_2}}}$$
For IIIrd part, $${n_3} = \frac{v}{{2{l_3}}} \Rightarrow {l_3} = \frac{v}{{2{n_3}}}$$
For the complete wire, $$n = \frac{v}{{2l}} \Rightarrow l = \frac{v}{{2n}}$$
We have, $$l = {l_1} + {l_2} + {l_3}$$
$$\eqalign{ & \frac{v}{{2n}} = \frac{v}{{2{n_1}}} + \frac{v}{{2{n_2}}} + \frac{v}{{2{n_3}}} \cr & \frac{1}{n} = \frac{1}{{{n_1}}} + \frac{1}{{{n_2}}} + \frac{1}{{{n_3}}} \cr} $$
In this problem, the fundamental frequencies of each part could be find. The fundamental frequency of the complete wire could be find. One should check each option for the given values.

For Ist part, $${n_1} = \frac{v}{{2{l_1}}} \Rightarrow {l_1} = \frac{v}{{2{n_1}}}$$
For IInd part, $${n_2} = \frac{v}{{2{l_2}}} \Rightarrow {l_2} = \frac{v}{{2{n_2}}}$$
For IIIrd part, $${n_3} = \frac{v}{{2{l_3}}} \Rightarrow {l_3} = \frac{v}{{2{n_3}}}$$
For the complete wire, $$n = \frac{v}{{2l}} \Rightarrow l = \frac{v}{{2n}}$$
We have, $$l = {l_1} + {l_2} + {l_3}$$
$$\eqalign{ & \frac{v}{{2n}} = \frac{v}{{2{n_1}}} + \frac{v}{{2{n_2}}} + \frac{v}{{2{n_3}}} \cr & \frac{1}{n} = \frac{1}{{{n_1}}} + \frac{1}{{{n_2}}} + \frac{1}{{{n_3}}} \cr} $$