Question
If $${I_1} = \int\limits_0^{\frac{\pi }{2}} {\cos \left( {\sin \,x} \right)dx\,;\,} {I_2} = \int\limits_0^{\frac{\pi }{2}} {\sin \left( {\cos \,x} \right)dx} $$ and $${I_3} = \int\limits_0^{\frac{\pi }{2}} {\cos \,x\,dx,} $$ then :
A.
$${I_1} > {I_3} > {I_2}$$
B.
$${I_3} > {I_1} > {I_2}$$
C.
$${I_1} > {I_2} > {I_3}$$
D.
$${I_3} > {I_2} > {I_1}$$
Answer :
$${I_1} > {I_3} > {I_2}$$
Solution :
$$\eqalign{ & {I_1} = \int\limits_0^{\frac{\pi }{2}} {\cos \left( {\sin \,x} \right)dx} \cr & {I_2} = \int\limits_0^{\frac{\pi }{2}} {\sin \left( {\cos \,x} \right)dx} \cr & {I_3} = \int\limits_0^{\frac{\pi }{2}} {\cos \,x\,dx} \cr} $$
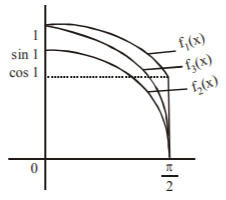
$$\eqalign{ & {\text{Let }}{f_1}\left( x \right) = \cos \left( {\sin \,x} \right),\,{f_2}\left( x \right) = \sin \left( {\cos \,x} \right),\,{f_3}\left( x \right) = \cos \,x \cr & {\text{If }}x > 0,{\text{ then }}\sin x < x \cr & \Rightarrow {\text{ for }}0 < x < \frac{\pi }{2}{\text{,}}\,{\text{sin}}\left( {\cos \,x} \right) < \cos \,x \cr & {\text{Also, }}0 < x < \frac{\pi }{2}{\text{ then }}\sin \,x < x \cr & \Rightarrow \cos \left( {\sin \,x} \right) > \cos \,x \cr & \therefore \,\cos \left( {\sin \,x} \right) > \cos \,x > \sin \left( {\cos \,x} \right){\text{ if }}0 < x < \frac{\pi }{2} \cr & \therefore \,{I_1} > {I_3} > {I_2} \cr} $$
$$\eqalign{ & {I_1} = \int\limits_0^{\frac{\pi }{2}} {\cos \left( {\sin \,x} \right)dx} \cr & {I_2} = \int\limits_0^{\frac{\pi }{2}} {\sin \left( {\cos \,x} \right)dx} \cr & {I_3} = \int\limits_0^{\frac{\pi }{2}} {\cos \,x\,dx} \cr} $$

$$\eqalign{ & {\text{Let }}{f_1}\left( x \right) = \cos \left( {\sin \,x} \right),\,{f_2}\left( x \right) = \sin \left( {\cos \,x} \right),\,{f_3}\left( x \right) = \cos \,x \cr & {\text{If }}x > 0,{\text{ then }}\sin x < x \cr & \Rightarrow {\text{ for }}0 < x < \frac{\pi }{2}{\text{,}}\,{\text{sin}}\left( {\cos \,x} \right) < \cos \,x \cr & {\text{Also, }}0 < x < \frac{\pi }{2}{\text{ then }}\sin \,x < x \cr & \Rightarrow \cos \left( {\sin \,x} \right) > \cos \,x \cr & \therefore \,\cos \left( {\sin \,x} \right) > \cos \,x > \sin \left( {\cos \,x} \right){\text{ if }}0 < x < \frac{\pi }{2} \cr & \therefore \,{I_1} > {I_3} > {I_2} \cr} $$