Question
If $$f\left( x \right) = a + bx + c{x^2},$$ where $$c > 0$$ and $${b^2} - 4ac < 0,$$ then the area enclosed by the coordinate axes, the line $$x = 2$$ and the curve $$y = f\left( x \right)$$ is given by :
A.
$$\frac{1}{3}\left\{ {4f\left( 1 \right) + f\left( 2 \right)} \right\}$$
B.
$$\frac{1}{2}\left\{ {f\left( 0 \right) + 4f\left( 1 \right) + f\left( 2 \right)} \right\}$$
C.
$$\frac{1}{2}\left\{ {f\left( 0 \right) + 4f\left( 1 \right)} \right\}$$
D.
$$\frac{1}{3}\left\{ {f\left( 0 \right) + 4f\left( 1 \right) + f\left( 2 \right)} \right\}$$
Answer :
$$\frac{1}{3}\left\{ {f\left( 0 \right) + 4f\left( 1 \right) + f\left( 2 \right)} \right\}$$
Solution :
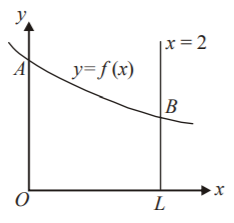
Area of $$OABL = \int_0^2 {y\,dx} $$
$$\eqalign{ & = \int_0^2 {\left( {a + bx + c{x^2}} \right)} dx \cr & = 2a + 2b + \frac{8}{3}c \cr & = \frac{1}{3}\left[ {6a + 6b + 8c} \right]......\left( {\text{i}} \right) \cr & {\text{But, }}f\left( x \right) = a + bx + c{x^2}\,; \cr & f\left( 0 \right) = a, \cr & f\left( 1 \right) = a + b + c \cr & f\left( 2 \right) = a + 2b + 4c \cr & \Rightarrow \frac{1}{3}\left\{ {f\left( 0 \right) + 4f\left( 1 \right) + f\left( 2 \right)} \right\} \cr & = \frac{1}{3}\left\{ {a + 4\left( {a + b + c} \right) + \left( {a + 2b + 4c} \right)} \right\} \cr & = \frac{1}{3}\left\{ {6a + 6b + 8c} \right\} \cr} $$

Area of $$OABL = \int_0^2 {y\,dx} $$
$$\eqalign{ & = \int_0^2 {\left( {a + bx + c{x^2}} \right)} dx \cr & = 2a + 2b + \frac{8}{3}c \cr & = \frac{1}{3}\left[ {6a + 6b + 8c} \right]......\left( {\text{i}} \right) \cr & {\text{But, }}f\left( x \right) = a + bx + c{x^2}\,; \cr & f\left( 0 \right) = a, \cr & f\left( 1 \right) = a + b + c \cr & f\left( 2 \right) = a + 2b + 4c \cr & \Rightarrow \frac{1}{3}\left\{ {f\left( 0 \right) + 4f\left( 1 \right) + f\left( 2 \right)} \right\} \cr & = \frac{1}{3}\left\{ {a + 4\left( {a + b + c} \right) + \left( {a + 2b + 4c} \right)} \right\} \cr & = \frac{1}{3}\left\{ {6a + 6b + 8c} \right\} \cr} $$