if c is the mid point of ab and p is any point outside ab

If $$C$$ is the mid point of $$AB$$ and $$P$$ is any point outside $$AB,$$ then :

A. $$\overrightarrow {PA} + \overrightarrow {PB} = 2\overrightarrow {PC} $$

B. $$\overrightarrow {PA} + \overrightarrow {PB} = \overrightarrow {PC} $$

C. $$\overrightarrow {PA} + \overrightarrow {PB} + 2\overrightarrow {PC} = \vec 0$$

D. $$\overrightarrow {PA} + \overrightarrow {PB} + \overrightarrow {PC} = \vec 0$$

Answer : $$\overrightarrow {PA} + \overrightarrow {PB} = 2\overrightarrow {PC} $$

Solution :
$$\eqalign{ & \overrightarrow {PA} + \overrightarrow {AP} = 0{\text{ and }}\overrightarrow {PC} + \overrightarrow {CP} = 0 \cr & \Rightarrow \overrightarrow {PA} + \overrightarrow {AC} + \overrightarrow {CP} = 0{\text{ and }}\overrightarrow {PB} + \overrightarrow {BC} + \overrightarrow {CP} = 0 \cr} $$
Adding, we get $$\overrightarrow {PA} + \overrightarrow {PB} + \overrightarrow {AC} + \overrightarrow {BC} + 2\overrightarrow {CP} = 0$$
Since $$\overrightarrow {AC} = - \overrightarrow {BC} \,\,\,{\text{& }}\,\,\overrightarrow {CP} = - \overrightarrow {PC} $$
$$ \Rightarrow \overrightarrow {PA} + \overrightarrow {PB} - 2\overrightarrow {PC} = 0$$
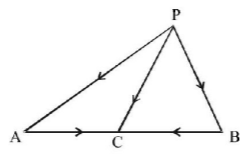
3D Geometry and Vectors mcq solution image

3D Geometry and Vectors mcq solution image

Releted MCQ Question on
Geometry >> 3D Geometry and Vectors

Releted Question 1

The scalar $$\vec A.\left( {\vec B + \vec C} \right) \times \left( {\vec A + \vec B + \vec C} \right)$$ equals :

A. $$0$$

B. $$\left[ {\vec A\,\vec B\,\vec C} \right] + \left[ {\vec B\,\vec C\,\vec A} \right]$$

C. $$\left[ {\vec A\,\vec B\,\vec C} \right]$$

D. None of these

View Answer

Releted Question 2

For non-zero vectors $$\vec a,\,\vec b,\,\vec c,\,\left| {\left( {\vec a \times \vec b} \right).\vec c} \right| = \left| {\vec a} \right|\left| {\vec b} \right|\left| {\vec c} \right|$$ holds if and only if -

A. $$\vec a.\vec b = 0,\,\,\,\vec b.\vec c = 0$$

B. $$\vec b.\vec c = 0,\,\,\,\vec c.\vec a = 0$$

C. $$\vec c.\vec a = 0,\,\,\,\vec a.\vec b = 0$$

D. $$\vec a.\vec b = \vec b.\vec c = \vec c.\vec a = 0$$

View Answer

Releted Question 3

The volume of the parallelepiped whose sides are given by $$\overrightarrow {OA} = 2i - 2j,\,\,\overrightarrow {OB} = i + j - k,\,\,\overrightarrow {OC} = 3i - k,$$ is :

A. $$\frac{4}{{13}}$$

B. $$4$$

C. $$\frac{2}{7}$$

D. none of these

View Answer

Releted Question 4

The points with position vectors $$60i + 3j,\,\,40i - 8j,\,\,ai - 52j$$ are collinear if :

A. $$a = - 40$$

B. $$a = 40$$

C. $$a = 20$$

D. none of these

View Answer

If $$C$$ is the mid point of $$AB$$ and $$P$$ is any point outside $$AB,$$ then :

Releted MCQ Question on
Geometry >> 3D Geometry and Vectors

The scalar $$\vec A.\left( {\vec B + \vec C} \right) \times \left( {\vec A + \vec B + \vec C} \right)$$ equals :

For non-zero vectors $$\vec a,\,\vec b,\,\vec c,\,\left| {\left( {\vec a \times \vec b} \right).\vec c} \right| = \left| {\vec a} \right|\left| {\vec b} \right|\left| {\vec c} \right|$$ holds if and only if -

The volume of the parallelepiped whose sides are given by $$\overrightarrow {OA} = 2i - 2j,\,\,\overrightarrow {OB} = i + j - k,\,\,\overrightarrow {OC} = 3i - k,$$ is :

The points with position vectors $$60i + 3j,\,\,40i - 8j,\,\,ai - 52j$$ are collinear if :

Practice More Releted MCQ Question on
3D Geometry and Vectors

Practice More MCQ Question on Maths Section

If $$C$$ is the mid point of $$AB$$ and $$P$$ is any point outside $$AB,$$ then :

Releted MCQ Question on Geometry >> 3D Geometry and Vectors

The scalar $$\vec A.\left( {\vec B + \vec C} \right) \times \left( {\vec A + \vec B + \vec C} \right)$$ equals :

For non-zero vectors $$\vec a,\,\vec b,\,\vec c,\,\left| {\left( {\vec a \times \vec b} \right).\vec c} \right| = \left| {\vec a} \right|\left| {\vec b} \right|\left| {\vec c} \right|$$ holds if and only if -

The volume of the parallelepiped whose sides are given by $$\overrightarrow {OA} = 2i - 2j,\,\,\overrightarrow {OB} = i + j - k,\,\,\overrightarrow {OC} = 3i - k,$$ is :

The points with position vectors $$60i + 3j,\,\,40i - 8j,\,\,ai - 52j$$ are collinear if :

Practice More Releted MCQ Question on 3D Geometry and Vectors

Practice More MCQ Question on Maths Section

Releted MCQ Question on
Geometry >> 3D Geometry and Vectors

Practice More Releted MCQ Question on
3D Geometry and Vectors