Question
If $$AB$$ is a double ordinate of the hyperbola $$\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1$$ such that $$\Delta OAB$$ is an equilateral triangle $$O$$ being the origin, then the eccentricity of the hyperbola satisfies :
A.
$$e > \sqrt 3 $$
B.
$$1 < e < \frac{2}{{\sqrt 3 }}$$
C.
$$e = \frac{2}{{\sqrt 3 }}$$
D.
$$e > \frac{2}{{\sqrt 3 }}$$
Answer :
$$e > \frac{2}{{\sqrt 3 }}$$
Solution :
Let the length of the double ordinate be $$2\ell $$
$$\therefore \,AB = 2\ell {\text{ and }}AM = BM = \ell $$
Clearly ordinate of point $$A$$ is $$\ell $$
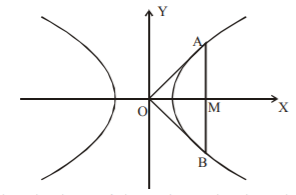
The abscissa of the point $$A$$ is given by
$$\eqalign{ & \frac{{{x^2}}}{{{a^2}}} - \frac{{{\ell ^2}}}{{{b^2}}} = 1 \Rightarrow x = \frac{{a\sqrt {{b^2} + {\ell ^2}} }}{b} \cr & \therefore \,A{\text{ is }}\left( {\frac{{a\sqrt {{b^2} + {\ell ^2}} }}{b},\,\ell } \right) \cr} $$
Since $$\Delta OAB$$ is equilateral triangle, therefore $$OA = AB = OB = 2\ell $$
Also, $$O{M^2} + A{M^2} = O{A^2}$$
$$\eqalign{ & \therefore \,\frac{{{a^2}\left( {{b^2} + {\ell ^2}} \right)}}{{{b^2}}} + {\ell ^2} = 4{\ell ^2} \cr & {\text{we get }}{\ell ^2} = \frac{{{a^2}{b^2}}}{{3{b^2} - {a^2}}} \cr & {\text{Since, }}{\ell ^2} > 0 \cr & \therefore \frac{{{a^2}{b^2}}}{{3{b^2} - {a^2}}} > 0 \cr & \Rightarrow 3{b^2} - {a^2} > 0 \cr & \Rightarrow 3{a^2}\left( {{e^2} - 1} \right) - {a^2} > 0 \cr & \Rightarrow e > \frac{2}{{\sqrt 3 }} \cr} $$
Let the length of the double ordinate be $$2\ell $$
$$\therefore \,AB = 2\ell {\text{ and }}AM = BM = \ell $$
Clearly ordinate of point $$A$$ is $$\ell $$

The abscissa of the point $$A$$ is given by
$$\eqalign{ & \frac{{{x^2}}}{{{a^2}}} - \frac{{{\ell ^2}}}{{{b^2}}} = 1 \Rightarrow x = \frac{{a\sqrt {{b^2} + {\ell ^2}} }}{b} \cr & \therefore \,A{\text{ is }}\left( {\frac{{a\sqrt {{b^2} + {\ell ^2}} }}{b},\,\ell } \right) \cr} $$
Since $$\Delta OAB$$ is equilateral triangle, therefore $$OA = AB = OB = 2\ell $$
Also, $$O{M^2} + A{M^2} = O{A^2}$$
$$\eqalign{ & \therefore \,\frac{{{a^2}\left( {{b^2} + {\ell ^2}} \right)}}{{{b^2}}} + {\ell ^2} = 4{\ell ^2} \cr & {\text{we get }}{\ell ^2} = \frac{{{a^2}{b^2}}}{{3{b^2} - {a^2}}} \cr & {\text{Since, }}{\ell ^2} > 0 \cr & \therefore \frac{{{a^2}{b^2}}}{{3{b^2} - {a^2}}} > 0 \cr & \Rightarrow 3{b^2} - {a^2} > 0 \cr & \Rightarrow 3{a^2}\left( {{e^2} - 1} \right) - {a^2} > 0 \cr & \Rightarrow e > \frac{2}{{\sqrt 3 }} \cr} $$