Releted MCQ Question on
Basic Physics >> Laws of Motion
Releted Question 1
A ship of mass $$3 \times {10^7}\,kg$$ initially at rest, is pulled by a force of $$5 \times {10^4}\,N$$ through a distance of $$3m.$$ Assuming that the resistance due to water is negligible, the speed of the ship is
A.
$$1.5 m/sec.$$
B.
$$60 m/sec.$$
C.
$$0.1 m/sec.$$
D.
$$5 m/sec.$$
Releted Question 2
The pulleys and strings shown in the figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle $$\theta $$ should be
The pulleys and strings shown in the figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle $$\theta $$ should be

A.
$${0^ \circ }$$
B.
$${30^ \circ }$$
C.
$${45^ \circ }$$
D.
$${60^ \circ }$$
Releted Question 3
A string of negligible mass going over a damped pulley of mass $$m$$ supports a block of mass $$M$$ as shown in the figure. The force on the pulley by the clamp is given by
A string of negligible mass going over a damped pulley of mass $$m$$ supports a block of mass $$M$$ as shown in the figure. The force on the pulley by the clamp is given by
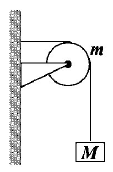
A.
$$\sqrt 2 \,{\text{Mg}}$$
B.
$$\sqrt 2 \,{\text{mg}}$$
C.
$$\sqrt {{{\left( {M + m} \right)}^2} + {m^2}} g$$
D.
$$\sqrt {{{\left( {M + m} \right)}^2} + {M^2}} g$$
Releted Question 4
The string between blocks of mass $$m$$ and $$2m$$ is massless and inextensible. The system is suspended by a massless spring as shown. If the string is cut find the magnitudes of accelerations of mass $$2m$$ and $$m$$ (immediately after cutting)
The string between blocks of mass $$m$$ and $$2m$$ is massless and inextensible. The system is suspended by a massless spring as shown. If the string is cut find the magnitudes of accelerations of mass $$2m$$ and $$m$$ (immediately after cutting)
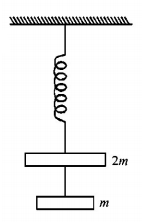
A.
g, g
B.
$$g,\frac{g}{2}$$
C.
$$\frac{g}{2},g$$
D.
$$\frac{g}{2},\frac{g}{2}$$