Question
If a particle is projected with speed $$u$$ from ground at an angle with horizontal ,then radius of curvature of a point where velocity vector is perpendicular to initial velocity vector is given by
A.
$$\frac{{{u^2}{{\cos }^2}\theta }}{g}$$
B.
$$\frac{{{u^2}{{\cot }^2}\theta }}{{g\sin \theta }}$$
C.
$$\frac{{{u^2}}}{g}$$
D.
$$\frac{{{u^2}{{\tan }^2}\theta }}{{g\cos \theta }}$$
Answer :
$$\frac{{{u^2}{{\cot }^2}\theta }}{{g\sin \theta }}$$
Solution :
Horizontal components of velocity at $$O$$ and $$P$$ are equal.
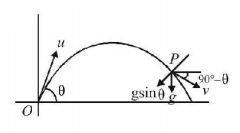
$$\eqalign{ & \therefore v\cos \left( {{{90}^ \circ } - \theta } \right) = u\cos \theta \cr & {\text{or}}\,\,v\sin \theta = u\cos \theta \cr & {\text{or}}\,v = u\cot \theta \cr & {\text{At}}\,\,P,\frac{{v_T^2}}{R} = {a_c}; \cr & \frac{{{u^2}{{\cot }^2}\theta }}{{g\sin \theta }} = R \cr} $$
Horizontal components of velocity at $$O$$ and $$P$$ are equal.

$$\eqalign{ & \therefore v\cos \left( {{{90}^ \circ } - \theta } \right) = u\cos \theta \cr & {\text{or}}\,\,v\sin \theta = u\cos \theta \cr & {\text{or}}\,v = u\cot \theta \cr & {\text{At}}\,\,P,\frac{{v_T^2}}{R} = {a_c}; \cr & \frac{{{u^2}{{\cot }^2}\theta }}{{g\sin \theta }} = R \cr} $$




