Question
If a direct current of value ampere is superimposed on an alternative current $$I = b\sin \omega t$$ flowing through a wire, what is the effective value of the resulting current in the circuit?
If a direct current of value ampere is superimposed on an alternative current $$I = b\sin \omega t$$ flowing through a wire, what is the effective value of the resulting current in the circuit?
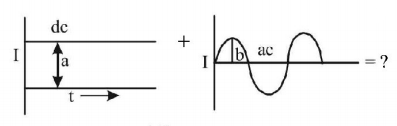
A.
$${\left[ {{a^2} - \frac{1}{2}{b^2}} \right]^{\frac{1}{2}}}$$
B.
$${\left[ {{a^2} + {b^2}} \right]^{\frac{1}{2}}}$$
C.
$${\left[ {\frac{{{a^2}}}{2} + {b^2}} \right]^{\frac{1}{2}}}$$
D.
$${\left[ {{a^2} + \frac{{{b^2}}}{2}} \right]^{\frac{1}{2}}}$$
Answer :
$${\left[ {{a^2} + \frac{{{b^2}}}{2}} \right]^{\frac{1}{2}}}$$
Solution :
as current any instant in the circuit will be
$$I = {I_{dc}} + {I_{ac}} = a + b\sin \omega t$$
$$\eqalign{ & {\text{so,}}\,\,{I_{{\text{eff}}}} = {\left[ {\frac{{\int_0^T {{I^2}dt} }}{{\int_0^T {dt} }}} \right]^{\frac{1}{2}}} = {\left[ {\frac{1}{T}\int_0^T {{{\left( {a + b\sin \omega t} \right)}^2}dt} } \right]^{\frac{1}{2}}} \cr & {\text{i}}{\text{.e}}{\text{.}}\,\,{I_{{\text{eff}}}} = {\left[ {\frac{1}{T}\int_0^T {{{\left( {{a^2} + 2ab\sin \omega t + {b^2}{{\sin }^2}\omega t} \right)}^2}dt} } \right]^{\frac{1}{2}}} \cr} $$
but as $$\frac{1}{T}\int_0^T {\sin \omega tdt} = 0\,{\text{and}}\,\frac{1}{T}\int_0^T {{{\sin }^2}\omega t\,dt = \frac{1}{2}} $$
So, $$\,{I_{{\text{eff}}}} = {\left[ {{a^2} + \frac{1}{2}{b^2}} \right]^{\frac{1}{2}}}$$
as current any instant in the circuit will be
$$I = {I_{dc}} + {I_{ac}} = a + b\sin \omega t$$
$$\eqalign{ & {\text{so,}}\,\,{I_{{\text{eff}}}} = {\left[ {\frac{{\int_0^T {{I^2}dt} }}{{\int_0^T {dt} }}} \right]^{\frac{1}{2}}} = {\left[ {\frac{1}{T}\int_0^T {{{\left( {a + b\sin \omega t} \right)}^2}dt} } \right]^{\frac{1}{2}}} \cr & {\text{i}}{\text{.e}}{\text{.}}\,\,{I_{{\text{eff}}}} = {\left[ {\frac{1}{T}\int_0^T {{{\left( {{a^2} + 2ab\sin \omega t + {b^2}{{\sin }^2}\omega t} \right)}^2}dt} } \right]^{\frac{1}{2}}} \cr} $$
but as $$\frac{1}{T}\int_0^T {\sin \omega tdt} = 0\,{\text{and}}\,\frac{1}{T}\int_0^T {{{\sin }^2}\omega t\,dt = \frac{1}{2}} $$
So, $$\,{I_{{\text{eff}}}} = {\left[ {{a^2} + \frac{1}{2}{b^2}} \right]^{\frac{1}{2}}}$$