Question
If $$\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c $$ are the position vectors of corners $$A,\,B,\,C$$ of a parallelogram $$ABCD,$$ then what is the position vector of the corner $$D\,?$$
A.
$$\overrightarrow a + \overrightarrow b + \overrightarrow c $$
B.
$$\overrightarrow a + \overrightarrow b - \overrightarrow c $$
C.
$$\overrightarrow a - \overrightarrow b + \overrightarrow c $$
D.
$$ - \overrightarrow a + \overrightarrow b + \overrightarrow c $$
Answer :
$$\overrightarrow a - \overrightarrow b + \overrightarrow c $$
Solution :
Let $$O$$ be the origin and $$ABCD$$ be the parallelogram.
$$\eqalign{ & \ln \,\Delta ODC, \cr & \overrightarrow {OD} = \overrightarrow {OC} + \overrightarrow {CD} \cr & \overrightarrow {CD} = - \overrightarrow {AB} \cr & {\text{and, }}\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} \,\,\left[ {\ln \,\Delta AOB} \right] \cr & = \overrightarrow b - \overrightarrow a \cr & {\text{Thus, }}\overrightarrow {CD} = - \overrightarrow {AB} = \overrightarrow a - \overrightarrow b \cr} $$
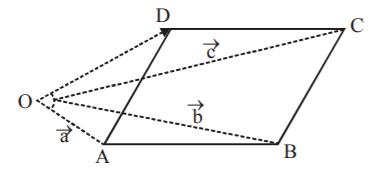
$$\eqalign{ & {\text{So, }}\overrightarrow {OD} = \overrightarrow c + \overrightarrow a - \overrightarrow b \cr & \left[ {{\text{since, }}\overrightarrow {OC} = \overrightarrow C {\text{ and }}\overrightarrow {CD} = \overrightarrow a - \overrightarrow b } \right] \cr} $$
Let $$O$$ be the origin and $$ABCD$$ be the parallelogram.
$$\eqalign{ & \ln \,\Delta ODC, \cr & \overrightarrow {OD} = \overrightarrow {OC} + \overrightarrow {CD} \cr & \overrightarrow {CD} = - \overrightarrow {AB} \cr & {\text{and, }}\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} \,\,\left[ {\ln \,\Delta AOB} \right] \cr & = \overrightarrow b - \overrightarrow a \cr & {\text{Thus, }}\overrightarrow {CD} = - \overrightarrow {AB} = \overrightarrow a - \overrightarrow b \cr} $$

$$\eqalign{ & {\text{So, }}\overrightarrow {OD} = \overrightarrow c + \overrightarrow a - \overrightarrow b \cr & \left[ {{\text{since, }}\overrightarrow {OC} = \overrightarrow C {\text{ and }}\overrightarrow {CD} = \overrightarrow a - \overrightarrow b } \right] \cr} $$