Question
If $$\overrightarrow a ,\,\overrightarrow b $$ and $$\overrightarrow c $$ are the position vectors of the vertices of an equilateral triangle whose orthocenter is at the origin, then which one of the following is correct ?
A.
$$\overrightarrow a + \overrightarrow b + \overrightarrow c = \overrightarrow 0 $$
B.
$$\overrightarrow a + \overrightarrow b + \overrightarrow c = {\text{unit vector}}$$
C.
$$\overrightarrow a + \overrightarrow b = \overrightarrow c $$
D.
$$\overrightarrow a = \overrightarrow b + \overrightarrow c $$
Answer :
$$\overrightarrow a + \overrightarrow b + \overrightarrow c = \overrightarrow 0 $$
Solution :
Position vectors of vertices $$A,\,B$$ and $$C$$ are $$\overrightarrow a ,\,\overrightarrow b $$ and $$\overrightarrow c .$$
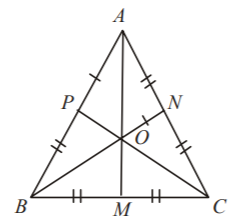
$$\because $$ triangle is equilateral.
$$\therefore $$ Centroid and orthocenter will coincide.
Centroid $$ \equiv $$ orthocenter position vector $$ = \frac{1}{3}\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)$$
$$\because $$ given in question orthocenter is at origin.
Hence, $$\frac{1}{3}\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right) = 0{\text{ or }}\overrightarrow a + \overrightarrow b + \overrightarrow c = 0$$
Position vectors of vertices $$A,\,B$$ and $$C$$ are $$\overrightarrow a ,\,\overrightarrow b $$ and $$\overrightarrow c .$$

$$\because $$ triangle is equilateral.
$$\therefore $$ Centroid and orthocenter will coincide.
Centroid $$ \equiv $$ orthocenter position vector $$ = \frac{1}{3}\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)$$
$$\because $$ given in question orthocenter is at origin.
Hence, $$\frac{1}{3}\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right) = 0{\text{ or }}\overrightarrow a + \overrightarrow b + \overrightarrow c = 0$$