Question
Gravitational field at the centre of a semicircle formed by a thin wire $$AB$$ of mass $$m$$ and length $$\ell $$ is
Gravitational field at the centre of a semicircle formed by a thin wire $$AB$$ of mass $$m$$ and length $$\ell $$ is
A.
$$\frac{{Gm}}{{{\ell ^2}}}$$ along $$+x$$ -axis
B.
$$\frac{{Gm}}{{\pi {\ell ^2}}}$$ along $$+y$$ -axis
C.
$$\frac{{2\pi Gm}}{{{\ell ^2}}}$$ along $$+x$$ -axis
D.
$$\frac{{2\pi Gm}}{{{\ell ^2}}}$$ along $$+y$$ -axis
Answer :
$$\frac{{2\pi Gm}}{{{\ell ^2}}}$$ along $$+y$$ -axis
Solution :
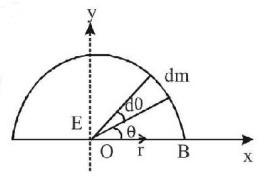
Let mass per unit light of wire, $$\lambda = \frac{m}{\ell }$$ and $$\pi r = \ell ,r = \frac{\ell }{\pi }.$$ mass of element, $$dm = \lambda \,rd\theta \,\,{\text{then}}\,\,dE = \frac{{Gdm}}{{{r^2}}}$$
$$\eqalign{ & \int\limits_0^\pi d E = \int\limits_0^\pi {\frac{{G\lambda rd\theta }}{{{r^2}}}} \left( {\widehat i\cos \theta + \widehat j\sin \theta } \right) \cr & E = \frac{{G\lambda }}{r}\left[ {\int\limits_0^\pi {\hat i} \cos \theta + \int\limits_0^\pi {\hat j} \sin \theta } \right] \cr & = \frac{{2G\lambda }}{r}\widehat j = \frac{{2GM}}{{\ell r}}\widehat j = \frac{{2Gm\pi }}{{{\ell ^2}}}\widehat j{\text{ }}\left( {{\text{along }}y - {\text{axis}}} \right) \cr} $$

Let mass per unit light of wire, $$\lambda = \frac{m}{\ell }$$ and $$\pi r = \ell ,r = \frac{\ell }{\pi }.$$ mass of element, $$dm = \lambda \,rd\theta \,\,{\text{then}}\,\,dE = \frac{{Gdm}}{{{r^2}}}$$
$$\eqalign{ & \int\limits_0^\pi d E = \int\limits_0^\pi {\frac{{G\lambda rd\theta }}{{{r^2}}}} \left( {\widehat i\cos \theta + \widehat j\sin \theta } \right) \cr & E = \frac{{G\lambda }}{r}\left[ {\int\limits_0^\pi {\hat i} \cos \theta + \int\limits_0^\pi {\hat j} \sin \theta } \right] \cr & = \frac{{2G\lambda }}{r}\widehat j = \frac{{2GM}}{{\ell r}}\widehat j = \frac{{2Gm\pi }}{{{\ell ^2}}}\widehat j{\text{ }}\left( {{\text{along }}y - {\text{axis}}} \right) \cr} $$