Given that $$x\, \in \left[ {0,\,1} \right]$$   and $$y\, \in \left[ {0,\,1} \right].$$   Let $$A$$ be the event of $$\left( {x,\,y} \right)$$  satisfying $${y^2} \leqslant x$$   and $$B$$ be the event of $$\left( {x,\,y} \right)$$  satisfying $${x^2} \leqslant y.$$   Then :

Solution :

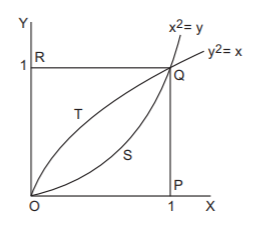
$$A =$$  the event of $$\left( {x,\,y} \right)$$  belonging to the area $$OTQPO$$
$$B =$$  the event of $$\left( {x,\,y} \right)$$  belonging to the area $$OSQRO$$
$$\eqalign{ & P\left( A \right) = \frac{{{\text{ar}}\left( {OTQPO} \right)}}{{{\text{ar}}\left( {OPQRO} \right)}} = \frac{{\int_0^1 {\sqrt x } \,dx}}{{1 \times 1}} = \left[ {\frac{2}{3}{x^{\frac{3}{2}}}} \right] = \frac{2}{3} \cr & P\left( B \right) = \frac{{{\text{ar}}\left( {OSQRO} \right)}}{{{\text{ar}}\left( {OPQRO} \right)}} = \frac{{\int_0^1 {\sqrt y } \,dy}}{{1 \times 1}} = \frac{2}{3} \cr & P\left( {A \cap B} \right) = \frac{{{\text{ar}}\left( {OTQS} \right)}}{{{\text{ar}}\left( {OPQRO} \right)}} = \frac{{\int_0^1 {\sqrt x } \,dx - \int_0^1 {{x^2}dx} }}{{1 \times 1}} = \frac{2}{3} - \frac{1}{3} = \frac{1}{3} \cr & P\left( A \right) + P\left( B \right) = \frac{2}{3} + \frac{2}{3} \ne 1. \cr & {\text{So, }}A{\text{ and }}B{\text{ are not exhaustive}}{\text{.}} \cr & P\left( A \right).P\left( B \right) = \frac{2}{3}.\frac{2}{3} = \frac{4}{9} \ne P\left( {A \cap B} \right). \cr & {\text{So, }}A{\text{ and }}B{\text{ are not independent}}{\text{.}} \cr & P\left( {A \cup B} \right) = 1,\,P\left( A \right) + P\left( B \right) = \frac{2}{3} + \frac{2}{3} \ne P\left( {A \cup B} \right). \cr & {\text{So, }}A{\text{ and }}B{\text{ are not mutually exclusive}}{\text{.}} \cr} $$