From the following bond energies
$$\eqalign{ & H - H\,{\text{bond energy}}:431.37\,kJ\,mo{l^{ - 1}} \cr & C = C\,{\text{bond energy}}:606.10\,kJ\,mo{l^{ - 1}} \cr & C - C\,{\text{bond energy}}:336.49\,kJ\,mo{l^{ - 1}} \cr & C - H\,{\text{bond energy}}:410.50\,kJ\,mo{l^{ - 1}}\, \cr} $$
Enthalpy for the reaction,

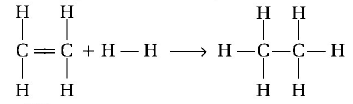
will be

Solution :
For reaction,

$$\Delta {H_{{\text{reaction}}}}$$   $$ = \sum {B{E_{\left( {{\text{reactant}}} \right)}}} - \sum {B{E_{\left( {{\text{product}}} \right)}}} ,$$       $$\left[ {BE = {\text{bond energy}}} \right]$$
$$\Delta {H_r} = $$   $$\left[ {4 \times B{E_{\left( {C - H} \right)}} + 1 \times B{E_{\left( {C = C} \right)}} + 1 \times B{E_{\left( {H - H} \right)}}} \right]$$         $$ - \left[ {6 \times B{E_{\left( {C - H} \right)}} + 1 \times B{E_{\left( {C - C} \right)}}} \right]$$
$$ = \left( {4 \times 410.50 + 1 \times 606.10 + 1 \times 431.37} \right)$$         $$ - \left[ {\left( {6 \times 410.50} \right) + \left( {1 \times 336.49} \right)} \right]kJ\,mo{l^{ - 1}}$$
$$ = \left[ {1642 + 606.1 + 431.37} \right]$$      $$ - \left[ {2463 + 336.49} \right]kJ\,mo{l^{ - 1}}$$
$$ = \left[ {2679.47} \right] - \left[ {2799.49} \right]\,kJ\,mo{l^{ - 1}}$$
$$ = - 120.0\,kJ\,mo{l^{ - 1}}$$