Question
From a solid sphere of mass $$M$$ and radius $$R$$ a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its center and perpendicular to one of its faces is:
A.
$$\frac{{4M{R^2}}}{{9\sqrt 3 \pi }}$$
B.
$$\frac{{4M{R^2}}}{{3\sqrt 3 \pi }}$$
C.
$$\frac{{M{R^2}}}{{32\sqrt 2 \pi }}$$
D.
$$\frac{{M{R^2}}}{{16\sqrt 2 \pi }}$$
Answer :
$$\frac{{4M{R^2}}}{{9\sqrt 3 \pi }}$$
Solution :
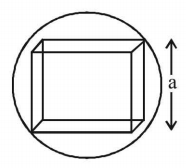
$$\eqalign{ & {\text{Here }}a = \frac{2}{{\sqrt 3 }}R \cr & {\text{Now, }}\frac{M}{{M'}} = \frac{{\frac{4}{3}\pi {R^3}}}{{{a^3}}} \cr & = \frac{{\frac{4}{3}\pi {R^3}}}{{{{\left( {\frac{2}{{\sqrt 3 }}R} \right)}^3}}} \cr & = \frac{{\sqrt 3 }}{2}\pi .\,\,\,\,\,\,\,\,\,\,M' = \frac{{2m}}{{\sqrt 3 \pi }} \cr} $$
Moment of inertia of the cube about the given axis,
$$I = \frac{{M'{a^2}}}{6} = \frac{{\frac{{2M}}{{\sqrt 3 \pi }} \times {{\left( {\frac{2}{{\sqrt 3 }}R} \right)}^2}}}{6} = \frac{{4M{R^2}}}{{9\sqrt 3 \pi}}$$

$$\eqalign{ & {\text{Here }}a = \frac{2}{{\sqrt 3 }}R \cr & {\text{Now, }}\frac{M}{{M'}} = \frac{{\frac{4}{3}\pi {R^3}}}{{{a^3}}} \cr & = \frac{{\frac{4}{3}\pi {R^3}}}{{{{\left( {\frac{2}{{\sqrt 3 }}R} \right)}^3}}} \cr & = \frac{{\sqrt 3 }}{2}\pi .\,\,\,\,\,\,\,\,\,\,M' = \frac{{2m}}{{\sqrt 3 \pi }} \cr} $$
Moment of inertia of the cube about the given axis,
$$I = \frac{{M'{a^2}}}{6} = \frac{{\frac{{2M}}{{\sqrt 3 \pi }} \times {{\left( {\frac{2}{{\sqrt 3 }}R} \right)}^2}}}{6} = \frac{{4M{R^2}}}{{9\sqrt 3 \pi}}$$