Question
From a point a metre above a lake the angle of elevation of a cloud is $$\alpha $$ and the angle of depression of its reflection is $$\beta .$$ The height of the cloud is
A.
$$\frac{{a\sin \left( {\alpha + \beta } \right)}}{{\sin \left( {\alpha - \beta } \right)}}{\text{metre}}$$
B.
$$\frac{{a\sin \left( {\alpha + \beta } \right)}}{{\sin \left( {\beta - \alpha } \right)}}{\text{metre}}$$
C.
$$\frac{{a\sin \left( {\alpha - \beta } \right)}}{{\sin \left( {\alpha + \beta } \right)}}{\text{metre}}$$
D.
None of these
Answer :
$$\frac{{a\sin \left( {\alpha + \beta } \right)}}{{\sin \left( {\beta - \alpha } \right)}}{\text{metre}}$$
Solution :
$$\left( {H + a} \right)\cot b = \left( {H - a} \right)\cot a$$
using componendo and dividendo
$$ \Rightarrow H = \frac{{a\sin \left( {\alpha + \beta } \right)}}{{\sin \left( {\beta - \alpha } \right)}}$$
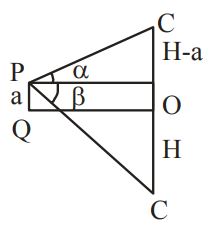
$$\left( {H + a} \right)\cot b = \left( {H - a} \right)\cot a$$
using componendo and dividendo
$$ \Rightarrow H = \frac{{a\sin \left( {\alpha + \beta } \right)}}{{\sin \left( {\beta - \alpha } \right)}}$$
