Question
From a disc of radius $$R$$ and mass $$M,$$ a circular hole of diameter $$R,$$ whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?
A.
$$\frac{{13\,M{R^2}}}{{32}}$$
B.
$$\frac{{11\,M{R^2}}}{{32}}$$
C.
$$\frac{{9\,M{R^2}}}{{32}}$$
D.
$$\frac{{15\,M{R^2}}}{{32}}$$
Answer :
$$\frac{{13\,M{R^2}}}{{32}}$$
Solution :
Considering the information given in the question, let us draw the figure
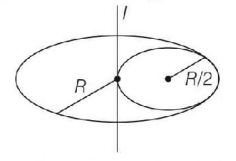
If the above figure is considered, then moment of inertia of disc will be given as
$$I = {I_{{\text{remain}}}} + {I_{\left( {\frac{R}{2}} \right)}} \Rightarrow {I_{{\text{remain}}}} = I - {I_{\left( {\frac{R}{2}} \right)}}$$
Putting the values, we get
$$\eqalign{ & = \frac{{M{R^2}}}{2} - \left[ {\frac{{\frac{M}{4}{{\left( {\frac{R}{2}} \right)}^2}}}{2} + \frac{M}{4}{{\left( {\frac{R}{2}} \right)}^2}} \right] \cr & = \frac{{M{R^2}}}{2} - \left[ {\frac{{M{R^2}}}{{32}} + \frac{{M{R^2}}}{{16}}} \right] \cr & = \frac{{M{R^2}}}{2} - \left[ {\frac{{M{R^2} + 2M{R^2}}}{{32}}} \right] \cr & = \frac{{M{R^2}}}{2} - \frac{{3M{R^2}}}{{32}} = \frac{{16M{R^2} - 3M{R^2}}}{{32}} \cr & {I_{{\text{remain }}}} = \frac{{13M{R^2}}}{{32}} \cr} $$
Considering the information given in the question, let us draw the figure

If the above figure is considered, then moment of inertia of disc will be given as
$$I = {I_{{\text{remain}}}} + {I_{\left( {\frac{R}{2}} \right)}} \Rightarrow {I_{{\text{remain}}}} = I - {I_{\left( {\frac{R}{2}} \right)}}$$
Putting the values, we get
$$\eqalign{ & = \frac{{M{R^2}}}{2} - \left[ {\frac{{\frac{M}{4}{{\left( {\frac{R}{2}} \right)}^2}}}{2} + \frac{M}{4}{{\left( {\frac{R}{2}} \right)}^2}} \right] \cr & = \frac{{M{R^2}}}{2} - \left[ {\frac{{M{R^2}}}{{32}} + \frac{{M{R^2}}}{{16}}} \right] \cr & = \frac{{M{R^2}}}{2} - \left[ {\frac{{M{R^2} + 2M{R^2}}}{{32}}} \right] \cr & = \frac{{M{R^2}}}{2} - \frac{{3M{R^2}}}{{32}} = \frac{{16M{R^2} - 3M{R^2}}}{{32}} \cr & {I_{{\text{remain }}}} = \frac{{13M{R^2}}}{{32}} \cr} $$