Question
From a circular disc of radius $$R$$ and mass $$9\,M,$$ a small disc of radius $$\frac{R}{3}$$ is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through $$O$$ is
From a circular disc of radius $$R$$ and mass $$9\,M,$$ a small disc of radius $$\frac{R}{3}$$ is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through $$O$$ is

A.
$$4M{R^2}$$
B.
$$\frac{{40}}{9}M{R^2}$$
C.
$$10M{R^2}$$
D.
$$\frac{{37}}{9}M{R^2}$$
Answer :
$$4M{R^2}$$
Solution :
Let $$\sigma $$ be the mass per unit area.
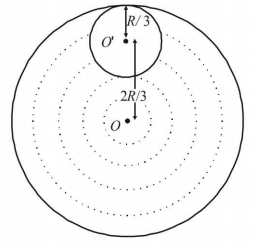
The total mass of the disc $$ = \sigma \times \pi {R^2} = 9M$$
The mass of the circular disc cut
$$ = \sigma \times \pi {\left( {\frac{R}{3}} \right)^2} = \sigma \times \frac{{\pi {R^2}}}{9} = M$$
Let us consider the above system as a complete disc of mass $$9\,M$$ and a negative mass $$M$$ super imposed on it.
Moment of inertia $$\left( {{I_1}} \right)$$ of the complete disc $$ = \frac{1}{2}9M{R^2}$$ about an axis passing through $$O$$ and perpendicular to the plane of the disc.
$$M.I.$$ of the cut out portion about an axis passing through $$O'$$ and perpendicular to the plane of disc $$ = \frac{1}{2} \times M \times {\left( {\frac{R}{3}} \right)^2}$$
$$\therefore \,\,M.I.\left( {{I_2}} \right)$$ of the cut out portion about an axis passing through $$O$$ and perpendicular to the plane of disc
$$ = \left[ {\frac{1}{2} \times M \times {{\left( {\frac{R}{3}} \right)}^2} + M \times {{\left( {\frac{{2R}}{3}} \right)}^2}} \right]$$ [Using perpendicular axis theorem]
$$\therefore $$ The total $$M.I.$$ of the system about an axis passing through $$O$$ and perpendicular to the plane of the disc is $$I = {I_1} + {I_2}$$
$$\eqalign{ & = \frac{1}{2}9M{R^2} - \left[ {\frac{1}{2} \times M \times {{\left( {\frac{R}{3}} \right)}^2} + M \times {{\left( {\frac{{2R}}{3}} \right)}^2}} \right] \cr & = \frac{{9M{R^2}}}{2} - \frac{{9M{R^2}}}{{18}} \cr & = \frac{{\left( {9 - 1} \right)M{R^2}}}{2} \cr & = 4\,M{R^2} \cr} $$
Let $$\sigma $$ be the mass per unit area.

The total mass of the disc $$ = \sigma \times \pi {R^2} = 9M$$
The mass of the circular disc cut
$$ = \sigma \times \pi {\left( {\frac{R}{3}} \right)^2} = \sigma \times \frac{{\pi {R^2}}}{9} = M$$
Let us consider the above system as a complete disc of mass $$9\,M$$ and a negative mass $$M$$ super imposed on it.
Moment of inertia $$\left( {{I_1}} \right)$$ of the complete disc $$ = \frac{1}{2}9M{R^2}$$ about an axis passing through $$O$$ and perpendicular to the plane of the disc.
$$M.I.$$ of the cut out portion about an axis passing through $$O'$$ and perpendicular to the plane of disc $$ = \frac{1}{2} \times M \times {\left( {\frac{R}{3}} \right)^2}$$
$$\therefore \,\,M.I.\left( {{I_2}} \right)$$ of the cut out portion about an axis passing through $$O$$ and perpendicular to the plane of disc
$$ = \left[ {\frac{1}{2} \times M \times {{\left( {\frac{R}{3}} \right)}^2} + M \times {{\left( {\frac{{2R}}{3}} \right)}^2}} \right]$$ [Using perpendicular axis theorem]
$$\therefore $$ The total $$M.I.$$ of the system about an axis passing through $$O$$ and perpendicular to the plane of the disc is $$I = {I_1} + {I_2}$$
$$\eqalign{ & = \frac{1}{2}9M{R^2} - \left[ {\frac{1}{2} \times M \times {{\left( {\frac{R}{3}} \right)}^2} + M \times {{\left( {\frac{{2R}}{3}} \right)}^2}} \right] \cr & = \frac{{9M{R^2}}}{2} - \frac{{9M{R^2}}}{{18}} \cr & = \frac{{\left( {9 - 1} \right)M{R^2}}}{2} \cr & = 4\,M{R^2} \cr} $$