Question
Four particles, each of mass $$M$$ and equidistant from each other, move along a circle of radius $$R$$ under the action of their mutual gravitational attraction. The speed of each particle is:
A.
$$\sqrt {\frac{{GM}}{R}} $$
B.
$$\sqrt {2\sqrt 2 \frac{{GM}}{R}} $$
C.
$$\sqrt {\frac{{GM}}{R}\left( {1 + 2\sqrt 2 } \right)} $$
D.
$$\frac{1}{2}\sqrt {\frac{{GM}}{R}\left( {1 + 2\sqrt 2 } \right)} $$
Answer :
$$\frac{1}{2}\sqrt {\frac{{GM}}{R}\left( {1 + 2\sqrt 2 } \right)} $$
Solution :
$$\eqalign{ & 2F\cos {45^ \circ } + F' = \frac{{M{v^2}}}{R}\left( {{\text{From figure}}} \right) \cr & {\text{Where }}F = \frac{{G{M^2}}}{{{{\left( {\sqrt 2 R} \right)}^2}}}{\text{ and }}F' = \frac{{G{M^2}}}{{4{R^2}}} \cr} $$
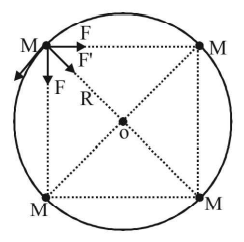
$$\eqalign{ & \Rightarrow \frac{{2 \times G{M^2}}}{{\sqrt 2 {{\left( {R\sqrt 2 } \right)}^2}}} + \frac{{G{M^2}}}{{4{R^2}}} = \frac{{M{v^2}}}{R} \cr & \Rightarrow \frac{{G{M^2}}}{R}\left[ {\frac{1}{4} + \frac{1}{{\sqrt 2 }}} \right] = M{v^2} \cr & \therefore v = \sqrt {\frac{{Gm}}{R}\left( {\frac{{\sqrt 2 + 4}}{{4\sqrt 2 }}} \right)} = \frac{1}{2}\sqrt {\frac{{Gm}}{R}\left( {1 + 2\sqrt 2 } \right)} \cr} $$
$$\eqalign{ & 2F\cos {45^ \circ } + F' = \frac{{M{v^2}}}{R}\left( {{\text{From figure}}} \right) \cr & {\text{Where }}F = \frac{{G{M^2}}}{{{{\left( {\sqrt 2 R} \right)}^2}}}{\text{ and }}F' = \frac{{G{M^2}}}{{4{R^2}}} \cr} $$

$$\eqalign{ & \Rightarrow \frac{{2 \times G{M^2}}}{{\sqrt 2 {{\left( {R\sqrt 2 } \right)}^2}}} + \frac{{G{M^2}}}{{4{R^2}}} = \frac{{M{v^2}}}{R} \cr & \Rightarrow \frac{{G{M^2}}}{R}\left[ {\frac{1}{4} + \frac{1}{{\sqrt 2 }}} \right] = M{v^2} \cr & \therefore v = \sqrt {\frac{{Gm}}{R}\left( {\frac{{\sqrt 2 + 4}}{{4\sqrt 2 }}} \right)} = \frac{1}{2}\sqrt {\frac{{Gm}}{R}\left( {1 + 2\sqrt 2 } \right)} \cr} $$