Question
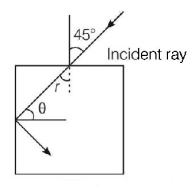
For the given incident ray as shown in figure, the condition of total internal reflection of the ray will be satisfied if the refractive index of block will be
For the given incident ray as shown in figure, the condition of total internal reflection of the ray will be satisfied if the refractive index of block will be
A.
$$\frac{{\sqrt 3 + 1}}{2}$$
B.
$$\frac{{\sqrt 2 + 1}}{2}$$
C.
$$\sqrt {\frac{3}{2}} $$
D.
$$\sqrt {\frac{7}{6}} $$
Answer :
$$\sqrt {\frac{3}{2}} $$
Solution :
For total internal reflection to take place,
angle of incidence > critical angle
i.e. $$\theta > C$$
or $$\sin \theta > \sin C$$
But for the case of total internal reflection,
$$\sin C = \frac{1}{\mu }$$
and according to question
$$\eqalign{ & \theta = {90^ \circ } - r \cr & {\text{So,}}\,\,\sin \left( {{{90}^ \circ } - r} \right) > \frac{1}{\mu } \cr & {\text{i}}{\text{.e}}{\text{.}}\,\mu > \frac{1}{{\cos r}}\,\,\left[ {\therefore \sin \left( {{{90}^ \circ } - r} \right) = \cos r} \right]\,......\left( {\text{i}} \right) \cr} $$
From Snell's law,
$$\eqalign{ & \frac{{\sin {{45}^ \circ }}}{{\sin r}} = \mu \cr & \Rightarrow \sin r = \frac{1}{{\sqrt 2 \mu }} \cr & \therefore \cos r = \sqrt {1 - {{\sin }^2}r} \cr & = \sqrt {1 - \frac{1}{{2{\mu ^2}}}} \cr} $$
Thus, Eq. (i) becomes
$$\eqalign{ & \mu > \frac{1}{{\sqrt {1 - \frac{1}{{2{\mu ^2}}}} }} \cr & \therefore {\mu ^2} = \frac{1}{{1 - \frac{1}{{2{\mu ^2}}}}} \cr & {\text{or}}\,\,{\mu ^2} - \frac{1}{2} = 1\,\,{\text{or}}\,\,\mu = \sqrt {\frac{3}{2}} \cr} $$
For total internal reflection to take place,
angle of incidence > critical angle
i.e. $$\theta > C$$
or $$\sin \theta > \sin C$$
But for the case of total internal reflection,
$$\sin C = \frac{1}{\mu }$$
and according to question
$$\eqalign{ & \theta = {90^ \circ } - r \cr & {\text{So,}}\,\,\sin \left( {{{90}^ \circ } - r} \right) > \frac{1}{\mu } \cr & {\text{i}}{\text{.e}}{\text{.}}\,\mu > \frac{1}{{\cos r}}\,\,\left[ {\therefore \sin \left( {{{90}^ \circ } - r} \right) = \cos r} \right]\,......\left( {\text{i}} \right) \cr} $$
From Snell's law,
$$\eqalign{ & \frac{{\sin {{45}^ \circ }}}{{\sin r}} = \mu \cr & \Rightarrow \sin r = \frac{1}{{\sqrt 2 \mu }} \cr & \therefore \cos r = \sqrt {1 - {{\sin }^2}r} \cr & = \sqrt {1 - \frac{1}{{2{\mu ^2}}}} \cr} $$
Thus, Eq. (i) becomes
$$\eqalign{ & \mu > \frac{1}{{\sqrt {1 - \frac{1}{{2{\mu ^2}}}} }} \cr & \therefore {\mu ^2} = \frac{1}{{1 - \frac{1}{{2{\mu ^2}}}}} \cr & {\text{or}}\,\,{\mu ^2} - \frac{1}{2} = 1\,\,{\text{or}}\,\,\mu = \sqrt {\frac{3}{2}} \cr} $$

