Question
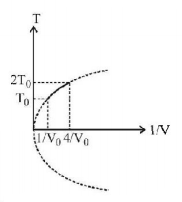
Figure shows a parabolic graph between $$T$$ and $$\frac{1}{V}$$ for a mixture of a gas undergoing an adiabatic process. What is the ratio of $${V_{rms}}$$ of molecules and speed of sound in mixture?
Figure shows a parabolic graph between $$T$$ and $$\frac{1}{V}$$ for a mixture of a gas undergoing an adiabatic process. What is the ratio of $${V_{rms}}$$ of molecules and speed of sound in mixture?
A.
$$\sqrt {\frac{3}{2}} $$
B.
$$\sqrt 2 $$
C.
$$\sqrt {\frac{2}{3}} $$
D.
$$\sqrt 3 $$
Answer :
$$\sqrt 2 $$
Solution :
From graph, $${T^2}V = {\text{const}}.\,\,......\left( {\text{i}} \right)$$
As we know that $$T{V^{\gamma - 1}} = {\text{const}}$$
$$ \Rightarrow V{T^{\frac{1}{{\gamma - 1}}}} = {\text{cons}}{\text{.}}\,......\left( {{\text{ii}}} \right)$$
On comparing (1) and (2), we get
$$\eqalign{ & \Rightarrow \gamma = \frac{3}{2} \cr & {\text{Also}}\,\,{v_{rms}} = \sqrt {\frac{{3P}}{\rho }} \,{\text{and}}\,{v_{{\text{sound}}}} = \sqrt {\frac{{P\gamma }}{\rho }} \cr} $$
$$ \Rightarrow \frac{{{v_{rms}}}}{{{v_{{\text{sound}}}}}} = \sqrt {\frac{3}{\gamma }} = \sqrt 2 $$
From graph, $${T^2}V = {\text{const}}.\,\,......\left( {\text{i}} \right)$$
As we know that $$T{V^{\gamma - 1}} = {\text{const}}$$
$$ \Rightarrow V{T^{\frac{1}{{\gamma - 1}}}} = {\text{cons}}{\text{.}}\,......\left( {{\text{ii}}} \right)$$
On comparing (1) and (2), we get
$$\eqalign{ & \Rightarrow \gamma = \frac{3}{2} \cr & {\text{Also}}\,\,{v_{rms}} = \sqrt {\frac{{3P}}{\rho }} \,{\text{and}}\,{v_{{\text{sound}}}} = \sqrt {\frac{{P\gamma }}{\rho }} \cr} $$
$$ \Rightarrow \frac{{{v_{rms}}}}{{{v_{{\text{sound}}}}}} = \sqrt {\frac{3}{\gamma }} = \sqrt 2 $$