Question
Energy levels $$A,B,C$$ of a certain atom correspond to increasing values of energy i.e. $${E_A} < {E_B} < {E_C}.$$ If $${\lambda _1},{\lambda _2},{\lambda _3}$$ are the wavelengths of radiation corresponding to the transitions $$C$$ to $$B,B$$ to $$A$$ and $$C$$ to $$A$$ respectively, which of the following relation is correct ?
A.
$${\lambda _3} = {\lambda _1} + {\lambda _2}$$
B.
$${\lambda _3} = \frac{{{\lambda _1}{\lambda _2}}}{{{\lambda _1} + {\lambda _2}}}$$
C.
$${\lambda _1} + {\lambda _2} + {\lambda _3} = 0$$
D.
$$\lambda _3^2 = \lambda _1^2 + \lambda _2^2$$
Answer :
$${\lambda _3} = \frac{{{\lambda _1}{\lambda _2}}}{{{\lambda _1} + {\lambda _2}}}$$
Solution :
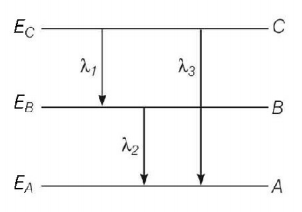
Using Bohr's postulate for radiation of spectral line, we have
Radiation of wavelength from $$C$$ to $$B$$
$${E_C} - {E_B} = \frac{{hc}}{{{\lambda _1}}}\,.......\left( {\text{i}} \right)$$
Radiation of wavelength from $$B$$ to $$A$$
$${E_B} - {E_A} = \frac{{hc}}{{{\lambda _2}}}\,.......\left( {{\text{ii}}} \right)$$
Radiation of wavelength from $$C$$ to $$A$$
$${E_C} - {E_A} = \frac{{hc}}{{{\lambda _3}}}\,.......\left( {{\text{iii}}} \right)$$
Also, $$\left( {{E_C} - {E_A}} \right) = \left( {{E_C} - {E_B}} \right) + \left( {{E_B} - {E_A}} \right)$$
$$\eqalign{ & \therefore \frac{{hc}}{{{\lambda _3}}} = \frac{{hc}}{{{\lambda _1}}} + \frac{{hc}}{{{\lambda _2}}}\, \cr & {\text{or}}\,\,\frac{1}{{{\lambda _3}}} = \frac{1}{{{\lambda _1}}} + \frac{1}{{{\lambda _2}}} \cr & \Rightarrow {\lambda _3} = \frac{{{\lambda _1}{\lambda _2}}}{{{\lambda _1} + {\lambda _2}}} \cr} $$

Using Bohr's postulate for radiation of spectral line, we have
Radiation of wavelength from $$C$$ to $$B$$
$${E_C} - {E_B} = \frac{{hc}}{{{\lambda _1}}}\,.......\left( {\text{i}} \right)$$
Radiation of wavelength from $$B$$ to $$A$$
$${E_B} - {E_A} = \frac{{hc}}{{{\lambda _2}}}\,.......\left( {{\text{ii}}} \right)$$
Radiation of wavelength from $$C$$ to $$A$$
$${E_C} - {E_A} = \frac{{hc}}{{{\lambda _3}}}\,.......\left( {{\text{iii}}} \right)$$
Also, $$\left( {{E_C} - {E_A}} \right) = \left( {{E_C} - {E_B}} \right) + \left( {{E_B} - {E_A}} \right)$$
$$\eqalign{ & \therefore \frac{{hc}}{{{\lambda _3}}} = \frac{{hc}}{{{\lambda _1}}} + \frac{{hc}}{{{\lambda _2}}}\, \cr & {\text{or}}\,\,\frac{1}{{{\lambda _3}}} = \frac{1}{{{\lambda _1}}} + \frac{1}{{{\lambda _2}}} \cr & \Rightarrow {\lambda _3} = \frac{{{\lambda _1}{\lambda _2}}}{{{\lambda _1} + {\lambda _2}}} \cr} $$