Question
Consider a tank made of glass (refractive index 1.5) with a thick bottom. It is filled with a liquid of refractive index $$\mu .$$ A student finds that, irrespective of what the incident angle $$i$$ (see figure) is for a beam of light entering the liquid, the light reflected from the liquid glass interface is never completely polarized. For this to happen, the minimum value of $$\mu $$ is :
Consider a tank made of glass (refractive index 1.5) with a thick bottom. It is filled with a liquid of refractive index $$\mu .$$ A student finds that, irrespective of what the incident angle $$i$$ (see figure) is for a beam of light entering the liquid, the light reflected from the liquid glass interface is never completely polarized. For this to happen, the minimum value of $$\mu $$ is :

A.
$$\sqrt {\frac{5}{3}} $$
B.
$$\frac{3}{{\sqrt 5 }}$$
C.
$$\frac{5}{{\sqrt 3 }}$$
D.
$$\frac{4}{3}$$
Answer :
$$\frac{3}{{\sqrt 5 }}$$
Solution :
For $$i \approx {90^ \circ }$$ at air liquid interface we have by Snell’s law
$$\eqalign{ & \mu = \frac{{\sin {{90}^ \circ }}}{{\sin r}} \cr & \therefore \,\,\sin r = \frac{1}{\mu } \cr} $$
According to Brewster’s law, refractive index of liquid $$\left( \mu \right)$$ is equal to tangent of polarising angle
$$\eqalign{ & \because \,\,\tan {i_b} = \frac{{1.5}}{\mu } \cr & \therefore \,\,\sin {i_b} = \frac{{1.5}}{{\sqrt {{\mu ^2} + {{1.5}^2}} }} \cr} $$
Here, $$\sin r < \sin {i_b}$$
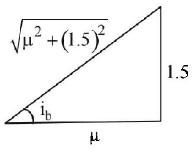
$$\eqalign{ & \therefore \,\,\frac{1}{\mu } \leqslant \frac{{1.5}}{{\sqrt {{\mu ^2} + {{\left( {1.5} \right)}^2}} }} \cr & {\text{or, }}\sqrt {{\mu ^2} + {{\left( {1.5} \right)}^2}} \leqslant 1.5 \times \mu \cr & \Rightarrow \,\,{\mu ^2} + {\left( {1.5} \right)^2} \leqslant {\left( {\mu \times 1.5} \right)^2} \cr & \Rightarrow \,\,\mu \geqslant \frac{3}{{\sqrt 5 }} \cr & {\text{i}}{\text{.e}}{\text{., minimum}} \cr} $$
value of $$\mu $$ should be $$\frac{3}{{\sqrt 5 }}$$
For $$i \approx {90^ \circ }$$ at air liquid interface we have by Snell’s law
$$\eqalign{ & \mu = \frac{{\sin {{90}^ \circ }}}{{\sin r}} \cr & \therefore \,\,\sin r = \frac{1}{\mu } \cr} $$
According to Brewster’s law, refractive index of liquid $$\left( \mu \right)$$ is equal to tangent of polarising angle
$$\eqalign{ & \because \,\,\tan {i_b} = \frac{{1.5}}{\mu } \cr & \therefore \,\,\sin {i_b} = \frac{{1.5}}{{\sqrt {{\mu ^2} + {{1.5}^2}} }} \cr} $$
Here, $$\sin r < \sin {i_b}$$

$$\eqalign{ & \therefore \,\,\frac{1}{\mu } \leqslant \frac{{1.5}}{{\sqrt {{\mu ^2} + {{\left( {1.5} \right)}^2}} }} \cr & {\text{or, }}\sqrt {{\mu ^2} + {{\left( {1.5} \right)}^2}} \leqslant 1.5 \times \mu \cr & \Rightarrow \,\,{\mu ^2} + {\left( {1.5} \right)^2} \leqslant {\left( {\mu \times 1.5} \right)^2} \cr & \Rightarrow \,\,\mu \geqslant \frac{3}{{\sqrt 5 }} \cr & {\text{i}}{\text{.e}}{\text{., minimum}} \cr} $$
value of $$\mu $$ should be $$\frac{3}{{\sqrt 5 }}$$