Question
Consider a system of two particles having masses $${m_1}$$ and $${m_2}.$$ If the particle of mass $${m_1}$$ is pushed towards the centre of mass of particles through a distance $$d,$$ by what distance would the particle of mass $${m_2}$$ move so as to keep the mass centre of particles at the original position?
A.
$$\frac{{{m_1}}}{{{m_1} + {m_2}}}d$$
B.
$$\frac{{{m_1}}}{{{m_2}}}d$$
C.
$$d$$
D.
$$\frac{{{m_2}}}{{{m_1}}}d$$
Answer :
$$\frac{{{m_1}}}{{{m_2}}}d$$
Solution :
The system of two given particles of masses $${m_1}$$ and $${m_2}$$ are shown in figure.
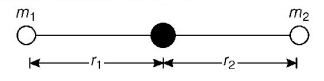
Initially the centre of mass $${r_{CM}} = \frac{{{m_1}{r_1} + {m_2}{r_2}}}{{{m_1} + {m_2}}}\,......\left( {\text{i}} \right)$$
When mass $${m_1}$$ moves towards centre of mass by a distance $$d,$$ then let mass $${m_2}$$ moves a distance $${d'}$$ away from $$CM$$ to keep the $$CM$$ in its initial position.
So, $${r_{CM}} = \frac{{{m_1}\left( {{r_1} - d} \right) + {m_2}\left( {{r_2} + d'} \right)}}{{{m_1} + {m_2}}}\,......\left( {{\text{ii}}} \right)$$
Equating Eqs. (i) and (ii), we get
$$\eqalign{ & \frac{{{m_1}{r_1} + {m_2}{r_2}}}{{{m_1} + {m_2}}} = \frac{{{m_1}\left( {{r_1} - d} \right) + {m_2}\left( {{r_2} + d'} \right)}}{{{m_1} + {m_2}}} \cr & \Rightarrow - {m_1}d + {m_2}d' = 0 \cr & \Rightarrow d' = \frac{{{m_1}}}{{{m_2}}}d. \cr} $$
NOTE
If both the masses are equal i.e., $${m_1} = {m_2},$$ then second mass will move a distance equal to the distance at which first mass is being displaced.
The system of two given particles of masses $${m_1}$$ and $${m_2}$$ are shown in figure.

Initially the centre of mass $${r_{CM}} = \frac{{{m_1}{r_1} + {m_2}{r_2}}}{{{m_1} + {m_2}}}\,......\left( {\text{i}} \right)$$
When mass $${m_1}$$ moves towards centre of mass by a distance $$d,$$ then let mass $${m_2}$$ moves a distance $${d'}$$ away from $$CM$$ to keep the $$CM$$ in its initial position.
So, $${r_{CM}} = \frac{{{m_1}\left( {{r_1} - d} \right) + {m_2}\left( {{r_2} + d'} \right)}}{{{m_1} + {m_2}}}\,......\left( {{\text{ii}}} \right)$$
Equating Eqs. (i) and (ii), we get
$$\eqalign{ & \frac{{{m_1}{r_1} + {m_2}{r_2}}}{{{m_1} + {m_2}}} = \frac{{{m_1}\left( {{r_1} - d} \right) + {m_2}\left( {{r_2} + d'} \right)}}{{{m_1} + {m_2}}} \cr & \Rightarrow - {m_1}d + {m_2}d' = 0 \cr & \Rightarrow d' = \frac{{{m_1}}}{{{m_2}}}d. \cr} $$
NOTE
If both the masses are equal i.e., $${m_1} = {m_2},$$ then second mass will move a distance equal to the distance at which first mass is being displaced.