Question
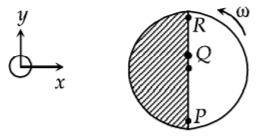
Consider a disc rotating in the horizontal plane with a constant angular speed $$\omega $$ about its centre $$O.$$ The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles $$P$$ and $$Q$$ are simultaneously projected at an angle towards $$R.$$ The velocity of projection is in the $$y-z$$ plane and is same for both pebbles with respect to the disc. Assume that $$\left( i \right)$$ they land back on the disc before the disc has completed $$\frac{1}{8}$$ rotation, $$\left( {ii} \right)$$ their range is less than half the disc radius, and $$\left( {iii} \right)$$ $$\omega $$ remains constant throughout. Then-
Consider a disc rotating in the horizontal plane with a constant angular speed $$\omega $$ about its centre $$O.$$ The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles $$P$$ and $$Q$$ are simultaneously projected at an angle towards $$R.$$ The velocity of projection is in the $$y-z$$ plane and is same for both pebbles with respect to the disc. Assume that $$\left( i \right)$$ they land back on the disc before the disc has completed $$\frac{1}{8}$$ rotation, $$\left( {ii} \right)$$ their range is less than half the disc radius, and $$\left( {iii} \right)$$ $$\omega $$ remains constant throughout. Then-
A.
$$P$$ lands in the shaded region and $$Q$$ in the unshaded region.
B.
$$P$$ lands in the unshaded region and $$Q$$ in the shaded region.
C.
Both $$P$$ and $$Q$$ land in the unshaded region.
D.
Both $$P$$ and $$Q$$ land in the shaded region.
Answer :
Both $$P$$ and $$Q$$ land in the unshaded region.
Solution :
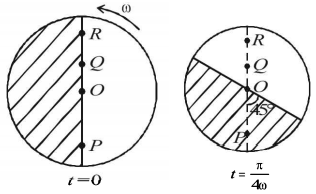
The x-coordinate of $$P = {v_x} \times t = \omega R \times \frac{\pi }{{4\omega }} = \frac{{\pi R}}{4}$$
This horizontal distance travelled will be greater than any point on the disc between $$O$$ and $$P.$$ Therefore the landing will be in unshaded area. In the same way, the horizontal distance travelled by $$Q$$ is always less than that of any point between $$O$$ and $$R.$$ Therefore the landing will be in unshaded area.

The x-coordinate of $$P = {v_x} \times t = \omega R \times \frac{\pi }{{4\omega }} = \frac{{\pi R}}{4}$$
This horizontal distance travelled will be greater than any point on the disc between $$O$$ and $$P.$$ Therefore the landing will be in unshaded area. In the same way, the horizontal distance travelled by $$Q$$ is always less than that of any point between $$O$$ and $$R.$$ Therefore the landing will be in unshaded area.




