Question
Consider a circle of radius $$R$$. What is the length of a chord which subtends an angle $$\theta $$ at the centre ?
A.
$$2R\,\sin \left( {\frac{\theta }{2}} \right)$$
B.
$$2R\,\sin \,\theta $$
C.
$$2R\,\tan \left( {\frac{\theta }{2}} \right)$$
D.
$$2R\,\tan \,\theta $$
Answer :
$$2R\,\sin \left( {\frac{\theta }{2}} \right)$$
Solution :
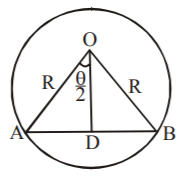
Let there be a circle of radius $$R$$ and $$AB$$ a chord.
$$\eqalign{ & OD \bot AB{\text{ and }}AD = DB \cr & {\text{and }}AB = 2AD \cr & \angle AOB = \theta \cr & \Rightarrow \angle AOD = \frac{\theta }{2} \cr & {\text{In }}\Delta AOD, \cr & \sin \,\frac{\theta }{2} = \frac{{AD}}{{OA}} \cr & \sin \,\frac{\theta }{2} = \frac{{AD}}{R} \cr & AD = R\,\sin \,\frac{\theta }{2} \cr} $$
$$\therefore $$ Length of chord $$AB = 2AD = 2R\,\sin \frac{\theta }{2}$$

Let there be a circle of radius $$R$$ and $$AB$$ a chord.
$$\eqalign{ & OD \bot AB{\text{ and }}AD = DB \cr & {\text{and }}AB = 2AD \cr & \angle AOB = \theta \cr & \Rightarrow \angle AOD = \frac{\theta }{2} \cr & {\text{In }}\Delta AOD, \cr & \sin \,\frac{\theta }{2} = \frac{{AD}}{{OA}} \cr & \sin \,\frac{\theta }{2} = \frac{{AD}}{R} \cr & AD = R\,\sin \,\frac{\theta }{2} \cr} $$
$$\therefore $$ Length of chord $$AB = 2AD = 2R\,\sin \frac{\theta }{2}$$