In all other molecules, $$N$$ and $$O$$ retain lone pair of electrons.

$$\eqalign{ & {\text{Bond order}} \cr & = \frac{{{\text{Number of bonds}}}}{{{\text{Number of Resonating structures}}}} \cr & = \frac{5}{4} = 1.25 \cr} $$
Three unit negative charge is being shared by four $$O$$  atoms. Formal charge $$ = - \frac{3}{4} = - 0.75$$

Canonical structures differ only in the position of electrons not in number of paired and unpaired electrons. All resonating structure must have the same number of valence electrons.

The value of lattice energy depends on the charges present on the two ions and the distance between them.

$$B{F_3}$$  is an electron deficient species, thus behaves like a Lewis acid.
$$\because {\text{Bond}}\,{\text{order}}\, = \frac{{{N_b} - {N_a}}}{2}$$

Bond order of $${N_2} = 3,N_2^ + = 2.5,N_2^ - = 2.5$$       and $$N_2^{2 - }$$  is 2. Higher the bond order, more is the stability.

(i) In $$N{a_2}{O_2},$$  we have $$O_2^{2 - }$$  ion. Number of valence electrons of the two oxygen in $$O_2^{2 - }$$ ion $$ = 8 \times 2 + 2 = 18$$    which are present as follows
$$\,\sigma 1{s^2},{\sigma ^*}1{s^2},\sigma 2{s^2},{\sigma ^*}2{s^2},\sigma 2p_x^2,$$      $$\left\{ {\pi 2p_y^2 = \pi 2p_z^2,\,\left\{ {{\pi ^*}2p_y^2 = {\pi ^*}2p_z^2} \right.} \right.$$
∴ Number of unpaired electrons $$\, = 0,$$  hence, $$O_2^{2 - }$$  is diamagnetic.
(ii) No. of valence electrons of all atoms in $$\,{O_3} = 6 \times 3 = 18.$$
Thus, it also, does not have any unpaired electron, hence it is diamagnetic.
(iii) No. of valence electrons of all atom in $$\,{N_2}O = 2 \times 5 + 6 = 16.$$     Hence, here also all electrons are paired. So it is diamagnetic.
(iv) In $$K{O_2}$$  we have $$O_2^ - $$  No. of valence electrons of all atoms in $$O_2^ - = 2 \times 6 + 1 = 13,$$
Thus it has one unpaired electron, hence it is paramagnetic.

In $$Br{F_3}$$  molecule, $$Br$$  is $$s{p^3}d$$  hybridised, but its geometry is $$T$$-shaped due to distortion of geometry from trigonal bipyramidal to $$T$$-shaped by the involvement of lone pair-lone pair repulsion.

Here, $$lp - lp\,\,{\text{repulsion}} = 0$$
         $$lp - bp\,\,{\text{repulsion}} = 4$$
         $$bp - bp\,\,{\text{repulsion}} = 2$$

Suppose the diatomic molecule is $$X.$$
Then, molecular orbital electronic configuration of
$${}_{16}X = \sigma 1{s^2},\mathop \sigma \limits^* 1{s^2},\sigma 2{s^2},\mathop \sigma \limits^* 2{s^2},$$       $$\sigma 2p_z^2,\pi 2p_x^2 \approx \pi 2p_y^2,\mathop \pi \limits^* 2p_x^1 \approx \mathop \pi \limits^* 2p_y^1$$
Due to presence of two unpaired electrons, it shows paramagnetic character.

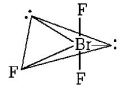
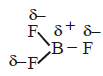The shape of $$B{F_3}$$  is trigonal planar and $$\mu = 0$$  hence it is non polar.
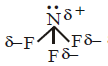The shape of $$N{F_3}$$  is pyramidal and $$\mu \ne 0$$  hence it is polar.