Question
Charges $$+ q$$ and $$- q$$ are placed at points $$A$$ and $$B$$ respectively which are a distance $$2L$$ apart, $$C$$ is the midpoint between $$A$$ and $$B.$$ The work done in moving a charge $$+Q$$ along the semicircle $$CRD$$ is
Charges $$+ q$$ and $$- q$$ are placed at points $$A$$ and $$B$$ respectively which are a distance $$2L$$ apart, $$C$$ is the midpoint between $$A$$ and $$B.$$ The work done in moving a charge $$+Q$$ along the semicircle $$CRD$$ is

A.
$$\frac{{qQ}}{{4\pi {\varepsilon _0}L}}$$
B.
$$\frac{{qQ}}{{2\pi {\varepsilon _0}L}}$$
C.
$$\frac{{qQ}}{{6\pi {\varepsilon _0}L}}$$
D.
$$ - \frac{{qQ}}{{6\pi {\varepsilon _0}L}}$$
Answer :
$$ - \frac{{qQ}}{{6\pi {\varepsilon _0}L}}$$
Solution :
In case I, when charge $$+Q$$ is situated at $$C.$$
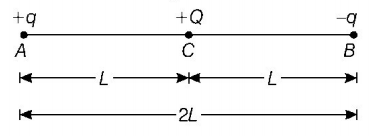
Electric potential energy of system,
$${U_1} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{{\left( q \right)\left( { - q} \right)}}{{2L}} + \frac{1}{{4\pi {\varepsilon _0}}}\frac{{\left( { - q} \right)Q}}{L} + \frac{1}{{4\pi {\varepsilon _0}}}\frac{{qQ}}{L}$$
In case II, when charge $$+Q$$ is moved from $$C$$ to $$D.$$
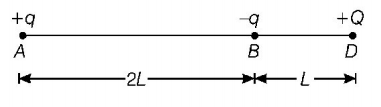
Electric potential energy of system in that case,
$${U_2} = \frac{1}{{4\pi {\varepsilon _0}}} \cdot \frac{{\left( q \right)\left( { - q} \right)}}{{2L}} + \frac{1}{{4\pi {\varepsilon _0}}} \cdot \frac{{qQ}}{{3L}} + \frac{1}{{4\pi {\varepsilon _0}}}\frac{{\left( { - q} \right)\left( Q \right)}}{L}$$
As we know that work done in moving a charge is equal to change in potential energy between the points it has been moved.
Work done, $$\Delta U = {U_2} - {U_1}$$
$$\eqalign{ & = \left( { - \frac{1}{{4\pi {\varepsilon _0}}}\frac{{{q^2}}}{{2L}} + \frac{1}{{4\pi {\varepsilon _0}}} \cdot \frac{{qQ}}{{3L}} - \frac{1}{{4\pi {\varepsilon _0}}}\frac{{qQ}}{L}} \right) - \left( { - \frac{1}{{4\pi {\varepsilon _0}}}\frac{{{q^2}}}{{2L}} - \frac{1}{{4\pi {\varepsilon _0}}} \cdot \frac{{qQ}}{L} + \frac{1}{{4\pi {\varepsilon _0}}}\frac{{qQ}}{L}} \right) \cr & = \frac{{qQ}}{{4\pi {\varepsilon _0}}} \cdot \left( {\frac{1}{{3L}} - \frac{1}{L}} \right) = \frac{{qQ}}{{4\pi {\varepsilon _0}}}\frac{{\left( {1 - 3} \right)}}{{3L}} \cr & = \frac{{ - 2qQ}}{{12\pi {\varepsilon _0}L}} = - \frac{{qQ}}{{6\pi {\varepsilon _0}L}} \cr} $$
In case I, when charge $$+Q$$ is situated at $$C.$$

Electric potential energy of system,
$${U_1} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{{\left( q \right)\left( { - q} \right)}}{{2L}} + \frac{1}{{4\pi {\varepsilon _0}}}\frac{{\left( { - q} \right)Q}}{L} + \frac{1}{{4\pi {\varepsilon _0}}}\frac{{qQ}}{L}$$
In case II, when charge $$+Q$$ is moved from $$C$$ to $$D.$$

Electric potential energy of system in that case,
$${U_2} = \frac{1}{{4\pi {\varepsilon _0}}} \cdot \frac{{\left( q \right)\left( { - q} \right)}}{{2L}} + \frac{1}{{4\pi {\varepsilon _0}}} \cdot \frac{{qQ}}{{3L}} + \frac{1}{{4\pi {\varepsilon _0}}}\frac{{\left( { - q} \right)\left( Q \right)}}{L}$$
As we know that work done in moving a charge is equal to change in potential energy between the points it has been moved.
Work done, $$\Delta U = {U_2} - {U_1}$$
$$\eqalign{ & = \left( { - \frac{1}{{4\pi {\varepsilon _0}}}\frac{{{q^2}}}{{2L}} + \frac{1}{{4\pi {\varepsilon _0}}} \cdot \frac{{qQ}}{{3L}} - \frac{1}{{4\pi {\varepsilon _0}}}\frac{{qQ}}{L}} \right) - \left( { - \frac{1}{{4\pi {\varepsilon _0}}}\frac{{{q^2}}}{{2L}} - \frac{1}{{4\pi {\varepsilon _0}}} \cdot \frac{{qQ}}{L} + \frac{1}{{4\pi {\varepsilon _0}}}\frac{{qQ}}{L}} \right) \cr & = \frac{{qQ}}{{4\pi {\varepsilon _0}}} \cdot \left( {\frac{1}{{3L}} - \frac{1}{L}} \right) = \frac{{qQ}}{{4\pi {\varepsilon _0}}}\frac{{\left( {1 - 3} \right)}}{{3L}} \cr & = \frac{{ - 2qQ}}{{12\pi {\varepsilon _0}L}} = - \frac{{qQ}}{{6\pi {\varepsilon _0}L}} \cr} $$