Question
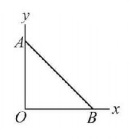
As per the diagram, a point charge $$+q$$ is placed at the origin $$O.$$ Work done in taking another point charge $$- Q$$ from the point $$A$$ [coordinates $$\left( {0,a} \right)$$ ] to another point $$B$$ [coordinates $$\left( {a,0} \right)$$ ] along the straight path $$AB$$ is:
As per the diagram, a point charge $$+q$$ is placed at the origin $$O.$$ Work done in taking another point charge $$- Q$$ from the point $$A$$ [coordinates $$\left( {0,a} \right)$$ ] to another point $$B$$ [coordinates $$\left( {a,0} \right)$$ ] along the straight path $$AB$$ is:
A.
zero
B.
$$\left( {\frac{{ - qQ}}{{4\pi {\varepsilon _0}}}\frac{1}{{{a^2}}}} \right)\sqrt 2 a$$
C.
$$\left( {\frac{{qQ}}{{4\pi {\varepsilon _0}}}\frac{1}{{{a^2}}}} \right).\frac{a}{{\sqrt 2 }}$$
D.
$$\left( {\frac{{qQ}}{{4\pi {\varepsilon _0}}}\frac{1}{{{a^2}}}} \right).\sqrt 2 a$$
Answer :
zero
Solution :
We know that potential energy of two charge system is given by
$$U = \frac{1}{{4\pi { \in _0}}}\frac{{{q_1}{q_2}}}{r}$$
According to question,
$$\eqalign{ & {U_A} = \frac{1}{{4\pi { \in _0}}}\frac{{\left( { + q} \right)\left( { - Q} \right)}}{a} = - \frac{1}{{4\pi {\varepsilon _0}}}\frac{{Qq}}{a} \cr & {\text{and}}\,{U_B} = \frac{1}{{4\pi { \in _0}}}\frac{{\left( { + q} \right)\left( { - Q} \right)}}{a} = - \frac{1}{{4\pi {\varepsilon _0}}}\frac{{Qq}}{a} \cr & \Delta U = {U_B} - {U_A} = 0 \cr} $$
We know that for conservative force,
$$W = - \Delta U = 0$$
We know that potential energy of two charge system is given by
$$U = \frac{1}{{4\pi { \in _0}}}\frac{{{q_1}{q_2}}}{r}$$
According to question,
$$\eqalign{ & {U_A} = \frac{1}{{4\pi { \in _0}}}\frac{{\left( { + q} \right)\left( { - Q} \right)}}{a} = - \frac{1}{{4\pi {\varepsilon _0}}}\frac{{Qq}}{a} \cr & {\text{and}}\,{U_B} = \frac{1}{{4\pi { \in _0}}}\frac{{\left( { + q} \right)\left( { - Q} \right)}}{a} = - \frac{1}{{4\pi {\varepsilon _0}}}\frac{{Qq}}{a} \cr & \Delta U = {U_B} - {U_A} = 0 \cr} $$
We know that for conservative force,
$$W = - \Delta U = 0$$