Question
Area bounded by the curves $$y = \left[ {\frac{{{x^2}}}{{64}} + 2} \right]$$ ( $$\left[ . \right]$$ denotes the greatest integer function ), $$v = x – 1$$ and $$x = 0,$$ above the $$x$$-axis is :
A.
2 square units
B.
3 square units
C.
4 square units
D.
None of these
Answer :
4 square units
Solution :
$$\eqalign{ & {\text{We have, }}0 \leqslant \frac{{{x^2}}}{{64}} < 1,{\text{ if}}\, - 8 < x < 8 \cr & \Rightarrow 2 \leqslant \frac{{{x^2}}}{{64}} + 2 < 3,{\text{ if }}\,\left| x \right| < 8 \cr & \Rightarrow y = \left[ {\frac{{{x^2}}}{{64}} + 2} \right] = 2,{\text{ if }}\,\left| x \right| < 8 \cr} $$
The graphs of the given curves is as shown in figure.
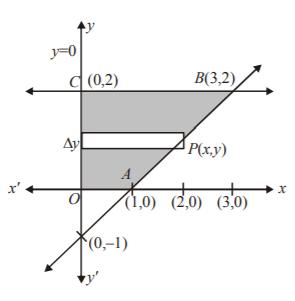
$$\eqalign{ & {\text{Required area}} = {\text{area of the shaded region}} \cr & = \int_0^2 {x\,dy} \cr & = \int_0^2 {\left( {y + 1} \right)dy} \cr & = \frac{1}{2}\left[ {\left( {y + 1} \right)} \right]_0^2 \cr & = \frac{9}{2} - \frac{1}{2} \cr & = 4{\text{ sq}}{\text{. units}} \cr} $$
$$\eqalign{ & {\text{We have, }}0 \leqslant \frac{{{x^2}}}{{64}} < 1,{\text{ if}}\, - 8 < x < 8 \cr & \Rightarrow 2 \leqslant \frac{{{x^2}}}{{64}} + 2 < 3,{\text{ if }}\,\left| x \right| < 8 \cr & \Rightarrow y = \left[ {\frac{{{x^2}}}{{64}} + 2} \right] = 2,{\text{ if }}\,\left| x \right| < 8 \cr} $$
The graphs of the given curves is as shown in figure.

$$\eqalign{ & {\text{Required area}} = {\text{area of the shaded region}} \cr & = \int_0^2 {x\,dy} \cr & = \int_0^2 {\left( {y + 1} \right)dy} \cr & = \frac{1}{2}\left[ {\left( {y + 1} \right)} \right]_0^2 \cr & = \frac{9}{2} - \frac{1}{2} \cr & = 4{\text{ sq}}{\text{. units}} \cr} $$