An observer can see through a pin - hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is $$3\,h$$  and its radius $$h.$$ When the beaker is filled with a liquid up to a height $$2\,h,$$  he can see the lower end of the rod. Then the refractive index of the liquid is

Solution :

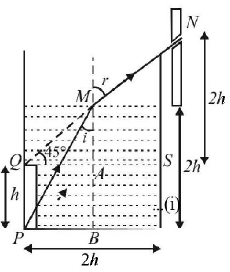
For the image of point $$P$$ to be seen by the observer, it should be formed at point $$Q.$$
In $$\Delta QNS,$$
$$\eqalign{ & NS = QS = 2\,h \cr & \therefore \,\,\angle NQS = {45^ \circ } \cr & \therefore \,\,r = {45^ \circ } \cr & {\text{Now in }}\Delta QMA, \cr & \angle MQA = {45^ \circ } \cr & \therefore \,MA = QA = h \cr & _2^1\mu = \frac{{\sin r}}{{\sin i}} = \frac{{\sin {{45}^ \circ }}}{{\sin i}} \cr & {\text{In }}\Delta PMB, \cr & P{M^2} = 4\,{h^2} + {h^2} \cr & = 5\,{h^2} \cr} $$
$$\therefore \,\,\sin i = \frac{h}{{\sqrt 5 h}} = \frac{1}{{\sqrt 5 }}\,\,\,\,.....\left( {{\text{ii}}} \right)$$
From (i) and (ii)
$$_2^1\mu = \sqrt {\frac{5}{2}} $$