Question
An $$LCR$$ circuit is equivalent to a damped pendulum. In an
$$LCR$$ circuit the capacitor is charged to $${Q_0}$$ and then connected to the $$L$$ and $$R$$ as shown below :
An $$LCR$$ circuit is equivalent to a damped pendulum. In an
$$LCR$$ circuit the capacitor is charged to $${Q_0}$$ and then connected to the $$L$$ and $$R$$ as shown below :

If a student plots graphs of the square of maximum charge
$$\left( {Q_{Max}^2} \right)$$ on the capacitor with time($$t$$) for two different values $${L_1}$$ and $${L_2}\left( {{L_1} > {L_2}} \right)$$ of $$L$$ then which of the following represents this graph correctly ? (plots are schematic and not drawn to scale)
A.


B.


C.


D.


Answer :


Solution :
From $$KVL$$ at any time $$t$$
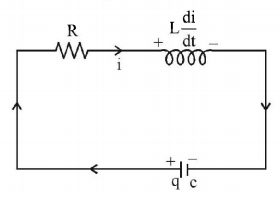
$$\eqalign{ & \frac{q}{c} - iR - L\frac{{di}}{{dt}} = 0 \cr & i = - \frac{{dq}}{{dt}} \Rightarrow \frac{q}{c} + \frac{{dq}}{{dt}}R + \frac{{L{d^2}q}}{{d{t^2}}} = 0 \cr & \frac{{{d^2}q}}{{d{t^2}}} + \frac{R}{L}\frac{{dq}}{{dt}} + \frac{q}{{Lc}} = 0 \cr} $$
From damped harmonic oscillator, the amplitude is given by $$A = {A_0}e - \frac{{dt}}{{2m}}$$
Double differential equation $$\frac{{{d^2}x}}{{d{t^2}}} + \frac{b}{m}\frac{{dx}}{{dt}} + \frac{k}{m}x = 0$$
$${Q_{\max }} = {Q_o}e - \frac{{Rt}}{{2L}} \Rightarrow Q_{\max }^2 = Q_o^2e - \frac{{Rt}}{L}$$
Hence damping will be faster for lesser self inductance.
From $$KVL$$ at any time $$t$$

$$\eqalign{ & \frac{q}{c} - iR - L\frac{{di}}{{dt}} = 0 \cr & i = - \frac{{dq}}{{dt}} \Rightarrow \frac{q}{c} + \frac{{dq}}{{dt}}R + \frac{{L{d^2}q}}{{d{t^2}}} = 0 \cr & \frac{{{d^2}q}}{{d{t^2}}} + \frac{R}{L}\frac{{dq}}{{dt}} + \frac{q}{{Lc}} = 0 \cr} $$
From damped harmonic oscillator, the amplitude is given by $$A = {A_0}e - \frac{{dt}}{{2m}}$$
Double differential equation $$\frac{{{d^2}x}}{{d{t^2}}} + \frac{b}{m}\frac{{dx}}{{dt}} + \frac{k}{m}x = 0$$
$${Q_{\max }} = {Q_o}e - \frac{{Rt}}{{2L}} \Rightarrow Q_{\max }^2 = Q_o^2e - \frac{{Rt}}{L}$$
Hence damping will be faster for lesser self inductance.
