Question
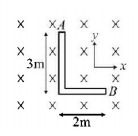
An $$L$$-shaped conductor rod is moving in transverse magnetic field as shown in the figure. Potential difference between ends of the rod is maximum if the rod is moving with velocity
An $$L$$-shaped conductor rod is moving in transverse magnetic field as shown in the figure. Potential difference between ends of the rod is maximum if the rod is moving with velocity
A.
$$4\hat i - 6\hat j\,m/s$$
B.
$$ - 4\hat i + 6\hat j\,m/s$$
C.
$$3\hat i + 2\hat j\,m/s$$
D.
$$\sqrt {13} \,\hat i\,m/s$$
Answer :
$$3\hat i + 2\hat j\,m/s$$
Solution :
For maximum potential difference the velocity must be perpendicular to the line $$AB,$$ and so
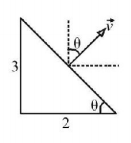
$$\eqalign{ & \overrightarrow v = v\sin \theta \hat i + v\cos \theta \hat j \cr & = v\left[ {\frac{3}{\ell }\hat i + \frac{2}{\ell }\hat j} \right] \cr & = \frac{v}{\ell }\left[ {3\hat i + 2\hat j} \right] \cr} $$
For maximum potential difference the velocity must be perpendicular to the line $$AB,$$ and so

$$\eqalign{ & \overrightarrow v = v\sin \theta \hat i + v\cos \theta \hat j \cr & = v\left[ {\frac{3}{\ell }\hat i + \frac{2}{\ell }\hat j} \right] \cr & = \frac{v}{\ell }\left[ {3\hat i + 2\hat j} \right] \cr} $$
