Question
An infinitesimally small bar magnet of dipole moment $$\overrightarrow M $$ is pointing and moving with the speed $$v$$ in the $${\hat x}$$- direction. A small closed circular conducting loop of radius $$a$$ and negligible self-inductance lies in the $$y-z$$ plane with its center at $$x =0,$$ and its axis coinciding with the $$x$$-axis. Find the force opposing the motion of the magnet, if the resistance of the loop is $$R.$$ Assume that the distance $$x$$ of the magnet from the center of the loop is much greater than $$a.$$
A.
$$\frac{{21}}{4}\frac{{\mu _0^2{M^2}{a^4}v}}{{R{x^8}}}$$
B.
$$\frac{{16}}{3}\frac{{{\mu _0}{M^2}{a^2}{v^2}}}{{R{x^3}}}$$
C.
$$\frac{3}{{23}}\frac{{{\mu _0}Ma{v^2}}}{{R{x^3}}}$$
D.
None of these
Answer :
$$\frac{{21}}{4}\frac{{\mu _0^2{M^2}{a^4}v}}{{R{x^8}}}$$
Solution :
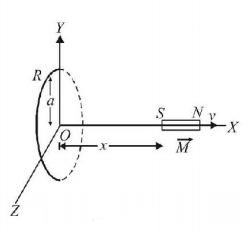
$$B = \frac{{{\mu _0}}}{{2\pi }}\frac{M}{{{x^3}}}$$
$$\therefore $$ Flux passing through the coil $$ = B{a^2}$$
$$\therefore $$ The induced emf in the coil
$$\eqalign{ & e = \frac{{ - d\phi }}{{dt}} = - \frac{d}{{dt}}\left[ {\frac{{{\mu _0}M{a^2}}}{2} \times \frac{1}{{{x^3}}}} \right] \cr & = \frac{{3{\mu _0}M{a^2}}}{{2{x^4}}}\frac{{dx}}{{dt}}\left[ {\because v = \frac{{dx}}{{dt}}} \right] \cr & = \frac{{3{\mu _0}M{a^2}}}{{2{x^4}}} \times v \cr} $$
$$\therefore $$ Current in the coil $$ = I = \frac{e}{R} = \frac{{3{\mu _0}M{a^2}v}}{{2{x^4}R}}$$
The magnetic moment of the loop
$$M' = I \times A = \frac{{3{\mu _0}M{a^2}v}}{{2{x^4}R}} \times {\left( {\pi a} \right)^2}$$
Now the potential energy of the loop placed in the magnetic field is
$$\eqalign{ & U = - M'B\cos {180^ \circ } = \frac{{3{\mu _0}M{a^2}v \times \pi {a^2}}}{{2{x^4}R}} \times \frac{{{\mu _0}M}}{{2\pi {x^3}}} \cr & \therefore U = \frac{{3\mu _0^2{M^2}{a^4}v}}{{4R{x^7}}} \cr & {\text{Now,}}\,\,\left| {\vec F} \right| = - \frac{{dU}}{{dx}} \cr & \therefore F = \frac{{21}}{4}\frac{{\mu _0^2{M^2}{a^4}v}}{{R{x^8}}} \cr} $$
Since by Newton’s third law, action and reaction are equal. Therefore, the above calculated force is acting on the magnet. The direction of the force is in $$ - \hat i$$ direction by Lenz’s law.

$$B = \frac{{{\mu _0}}}{{2\pi }}\frac{M}{{{x^3}}}$$
$$\therefore $$ Flux passing through the coil $$ = B{a^2}$$
$$\therefore $$ The induced emf in the coil
$$\eqalign{ & e = \frac{{ - d\phi }}{{dt}} = - \frac{d}{{dt}}\left[ {\frac{{{\mu _0}M{a^2}}}{2} \times \frac{1}{{{x^3}}}} \right] \cr & = \frac{{3{\mu _0}M{a^2}}}{{2{x^4}}}\frac{{dx}}{{dt}}\left[ {\because v = \frac{{dx}}{{dt}}} \right] \cr & = \frac{{3{\mu _0}M{a^2}}}{{2{x^4}}} \times v \cr} $$
$$\therefore $$ Current in the coil $$ = I = \frac{e}{R} = \frac{{3{\mu _0}M{a^2}v}}{{2{x^4}R}}$$
The magnetic moment of the loop
$$M' = I \times A = \frac{{3{\mu _0}M{a^2}v}}{{2{x^4}R}} \times {\left( {\pi a} \right)^2}$$
Now the potential energy of the loop placed in the magnetic field is
$$\eqalign{ & U = - M'B\cos {180^ \circ } = \frac{{3{\mu _0}M{a^2}v \times \pi {a^2}}}{{2{x^4}R}} \times \frac{{{\mu _0}M}}{{2\pi {x^3}}} \cr & \therefore U = \frac{{3\mu _0^2{M^2}{a^4}v}}{{4R{x^7}}} \cr & {\text{Now,}}\,\,\left| {\vec F} \right| = - \frac{{dU}}{{dx}} \cr & \therefore F = \frac{{21}}{4}\frac{{\mu _0^2{M^2}{a^4}v}}{{R{x^8}}} \cr} $$
Since by Newton’s third law, action and reaction are equal. Therefore, the above calculated force is acting on the magnet. The direction of the force is in $$ - \hat i$$ direction by Lenz’s law.
