Question
An ideal gas enclosed in a vertical cylindrical container supports a freely moving piston of mass $$M.$$ The piston and the cylinder have equal cross sectional area $$A.$$ When the piston is in equilibrium, the volume of the gas is $${V_0}$$ and its pressure is $${P_0.}$$ The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
A.
$$\frac{1}{{2\pi }}\frac{{A\gamma {P_0}}}{{{V_0}M}}$$
B.
$$\frac{1}{{2\pi }}\frac{{{V_0}M{P_0}}}{{{A^2}\gamma }}$$
C.
$$\frac{1}{{2\pi }}\sqrt {\frac{{{A^2}\gamma {P_0}}}{{MV}}} $$
D.
$$\frac{1}{{2\pi }}\sqrt {\frac{{M{V_0}}}{{A\gamma {P_0}}}} $$
Answer :
$$\frac{1}{{2\pi }}\sqrt {\frac{{{A^2}\gamma {P_0}}}{{MV}}} $$
Solution :
$$\eqalign{ & \frac{{Mg}}{A} = {P_0}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{P_0}V_0^\gamma = P{V^\gamma } \cr & Mg = {P_0}A\,......\left( 1 \right)\,\,\,\,\,\,\,\,\,\,\,{P_0}Ax_0^\gamma = PA{\left( {{x_0} - x} \right)^\gamma } \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,P = \frac{{{P_0}x_0^\gamma }}{{{{\left( {{x_0} - x} \right)}^\gamma }}} \cr} $$
Let piston is displaced by distance $$x$$
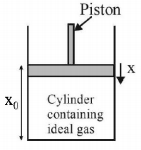
$$\eqalign{ & Mg - \left( {\frac{{{P_0}x_0^\gamma }}{{{{\left( {{x_0} - x} \right)}^\gamma }}}} \right)A = {F_{{\text{restoring }}}} \cr & {P_0}A\left( {1 - \frac{{x_0^\gamma }}{{{{\left( {{x_0} - x} \right)}^\gamma }}}} \right) = {F_{{\text{restoring }}}}\,\left[ {{x_0} - x \approx {x_0}} \right] \cr & F = - \frac{{\gamma {P_0}Ax}}{{{x_0}}} \cr} $$
$$\therefore $$ Frequency with which piston executes SHM.
$$f = \frac{1}{{2\pi }}\sqrt {\frac{{\gamma {P_0}A}}{{{x_0}M}}} = \frac{1}{{2\pi }}\sqrt {\frac{{\gamma {P_0}{A^2}}}{{M{V_0}}}} $$
$$\eqalign{ & \frac{{Mg}}{A} = {P_0}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{P_0}V_0^\gamma = P{V^\gamma } \cr & Mg = {P_0}A\,......\left( 1 \right)\,\,\,\,\,\,\,\,\,\,\,{P_0}Ax_0^\gamma = PA{\left( {{x_0} - x} \right)^\gamma } \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,P = \frac{{{P_0}x_0^\gamma }}{{{{\left( {{x_0} - x} \right)}^\gamma }}} \cr} $$
Let piston is displaced by distance $$x$$

$$\eqalign{ & Mg - \left( {\frac{{{P_0}x_0^\gamma }}{{{{\left( {{x_0} - x} \right)}^\gamma }}}} \right)A = {F_{{\text{restoring }}}} \cr & {P_0}A\left( {1 - \frac{{x_0^\gamma }}{{{{\left( {{x_0} - x} \right)}^\gamma }}}} \right) = {F_{{\text{restoring }}}}\,\left[ {{x_0} - x \approx {x_0}} \right] \cr & F = - \frac{{\gamma {P_0}Ax}}{{{x_0}}} \cr} $$
$$\therefore $$ Frequency with which piston executes SHM.
$$f = \frac{1}{{2\pi }}\sqrt {\frac{{\gamma {P_0}A}}{{{x_0}M}}} = \frac{1}{{2\pi }}\sqrt {\frac{{\gamma {P_0}{A^2}}}{{M{V_0}}}} $$