Question
An equilateral triangle is inscribed in the circle $${x^2} + {y^2} = {a^2}$$ with one of the vertices at $$\left( {a,\,0} \right).$$ What is the equation of the side opposite to this vertex ?
A.
$$2x - a = 0$$
B.
$$x + a = 0$$
C.
$$2x + a = 0$$
D.
$$3x - 2a = 0$$
Answer :
$$2x + a = 0$$
Solution :
Since the equilateral triangle is inscribed in the circle with centre at the origin, centroid lies on the origin.
So, $$\frac{{AO}}{{OD}} = \frac{2}{1}$$ and $$OD = \frac{1}{2}AO = \frac{a}{2}$$
So, other vertices of triangle have coordinates,
$$\left( { - \frac{a}{2},\,\frac{{\sqrt {3a} }}{2}} \right){\text{ and }}\left[ { - \frac{a}{2},\, - \frac{{\sqrt 3 }}{2}a} \right]$$
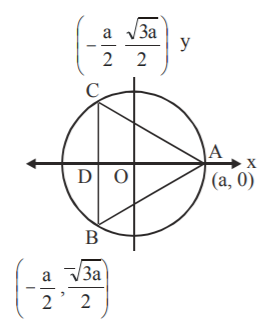
$$\therefore $$ Equation of line $$BC$$ is :
$$x = - \frac{a}{2}\, \Rightarrow 2x + a = 0$$
Since the equilateral triangle is inscribed in the circle with centre at the origin, centroid lies on the origin.
So, $$\frac{{AO}}{{OD}} = \frac{2}{1}$$ and $$OD = \frac{1}{2}AO = \frac{a}{2}$$
So, other vertices of triangle have coordinates,
$$\left( { - \frac{a}{2},\,\frac{{\sqrt {3a} }}{2}} \right){\text{ and }}\left[ { - \frac{a}{2},\, - \frac{{\sqrt 3 }}{2}a} \right]$$
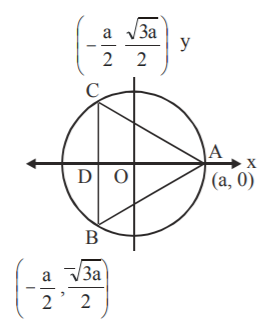
$$\therefore $$ Equation of line $$BC$$ is :
$$x = - \frac{a}{2}\, \Rightarrow 2x + a = 0$$