Question
An electric charge $${10^{ - 3}}\mu C$$ is placed at the origin (0, 0) of $$X - Y$$ co-ordinate system. Two points $$A$$ and $$B$$ are situated at $$\left( {\sqrt 2 ,\sqrt 2 } \right)$$ and (2, 0) respectively. The potential difference between the points $$A$$ and $$B$$ will be
A.
$$4.5\,volts$$
B.
$$9\,volts$$
C.
Zero
D.
$$2\,volt$$
Answer :
Zero
Solution :
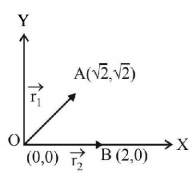
The distance of point $$A\left( {\sqrt 2 ,\sqrt 2 } \right)$$ from the origin,
$$OA = \left| {{{\vec r}_1}} \right| = \sqrt {{{\left( {\sqrt 2 } \right)}^2} + {{\left( {\sqrt 2 } \right)}^2}} = \sqrt 4 = 2\,units.$$
The distance of point $$B\left( {2,0} \right)$$ from the origin,
$$OB = \left| {{{\vec r}_2}} \right| = \sqrt {{{\left( 2 \right)}^2} + {{\left( 0 \right)}^2}} = 2\,units.$$
Now, potential at $$A,{V_A} = \frac{1}{{4\pi { \in _0}}} \cdot \frac{Q}{{\left( {OA} \right)}}$$
Potential at $$B,{V_B} = \frac{1}{{4\pi { \in _0}}} \cdot \frac{Q}{{\left( {OB} \right)}}$$
$$\therefore $$ Potential difference between the points $$A$$ and $$B$$ is zero.

The distance of point $$A\left( {\sqrt 2 ,\sqrt 2 } \right)$$ from the origin,
$$OA = \left| {{{\vec r}_1}} \right| = \sqrt {{{\left( {\sqrt 2 } \right)}^2} + {{\left( {\sqrt 2 } \right)}^2}} = \sqrt 4 = 2\,units.$$
The distance of point $$B\left( {2,0} \right)$$ from the origin,
$$OB = \left| {{{\vec r}_2}} \right| = \sqrt {{{\left( 2 \right)}^2} + {{\left( 0 \right)}^2}} = 2\,units.$$
Now, potential at $$A,{V_A} = \frac{1}{{4\pi { \in _0}}} \cdot \frac{Q}{{\left( {OA} \right)}}$$
Potential at $$B,{V_B} = \frac{1}{{4\pi { \in _0}}} \cdot \frac{Q}{{\left( {OB} \right)}}$$
$$\therefore $$ Potential difference between the points $$A$$ and $$B$$ is zero.

