Question
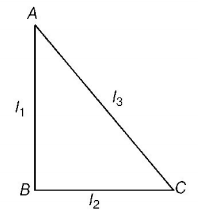
$$ABC$$ is a right angled triangular plate of uniform thickness. The sides are such that $$AB > BC$$ as shown in figure. $${I_1},{I_1},{I_3}$$ are moments of inertia about $$AB,\,BC$$ and $$AC$$ respectively. Then, which of the following relations is correct?
$$ABC$$ is a right angled triangular plate of uniform thickness. The sides are such that $$AB > BC$$ as shown in figure. $${I_1},{I_1},{I_3}$$ are moments of inertia about $$AB,\,BC$$ and $$AC$$ respectively. Then, which of the following relations is correct?
A.
$${I_1} = {I_1} = {I_3}$$
B.
$${I_2} > {I_1} > {I_3}$$
C.
$${I_3} < {I_2} < {I_1}$$
D.
$${I_3} > {I_1} > {I_2}$$
Answer :
$${I_2} > {I_1} > {I_3}$$
Solution :
The moment of inertia of a body about an axis depends not only on the mass of the body, but also on the distribution of mass from the axis. For a given body, mass is same, so it will depend only on the distribution of mass from the axis.
The mass is farthest from axis $$BC,$$ so $${I_2}$$ is maximum. Mass is nearest to axis $$AC,$$ so $${I_3}$$ is minimum. Hence, the correct sequence will be $${I_2} > {I_1} > {I_3}$$
NOTE
In a rotational motion, moment of inertia is also known as rotational inertia.
The moment of inertia of a body about an axis depends not only on the mass of the body, but also on the distribution of mass from the axis. For a given body, mass is same, so it will depend only on the distribution of mass from the axis.
The mass is farthest from axis $$BC,$$ so $${I_2}$$ is maximum. Mass is nearest to axis $$AC,$$ so $${I_3}$$ is minimum. Hence, the correct sequence will be $${I_2} > {I_1} > {I_3}$$
NOTE
In a rotational motion, moment of inertia is also known as rotational inertia.