Question
A wire carrying current $$I$$ has the shape as shown in adjoining figure. Linear parts of the wire are very long and parallel to $$X$$-axis while semicircular portion of radius $$R$$ is lying in $$Y-Z$$ plane. Magnetic field at point $$O$$ is :
A wire carrying current $$I$$ has the shape as shown in adjoining figure. Linear parts of the wire are very long and parallel to $$X$$-axis while semicircular portion of radius $$R$$ is lying in $$Y-Z$$ plane. Magnetic field at point $$O$$ is :
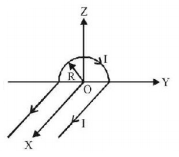
A.
$$\overrightarrow B = - \frac{{{\mu _0}}}{{4\pi }}\frac{I}{R}\left( {\mu \hat i \times 2\hat k} \right)$$
B.
$$\overrightarrow B = - \frac{{{\mu _0}}}{{4\pi }}\frac{I}{R}\left( {\pi \hat i + 2\hat k} \right)$$
C.
$$\overrightarrow B = \frac{{{\mu _0}}}{{4\pi }}\frac{I}{R}\left( {\pi \hat i - 2\hat k} \right)$$
D.
$$\overrightarrow B = \frac{{{\mu _0}}}{{4\pi }}\frac{I}{R}\left( {\pi \hat i + 2\hat k} \right)$$
Answer :
$$\overrightarrow B = - \frac{{{\mu _0}}}{{4\pi }}\frac{I}{R}\left( {\pi \hat i + 2\hat k} \right)$$
Solution :
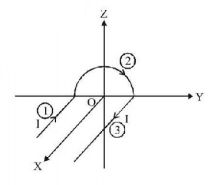
Magnetic field due to segment '1'
$$\eqalign{ & \overrightarrow {{B_1}} = \frac{{{\mu _0}I}}{{4\pi R}}\,\left[ {\sin {{90}^ \circ } + \sin {0^ \circ }} \right]\left( { - \hat k} \right) \cr & = \frac{{ - {\mu _0}I}}{{4\pi R}}\left( {\hat k} \right) = \overrightarrow {{B_3}} \cr} $$
Magnetic field due to segment '2'
$$\eqalign{ & {B_2} = \frac{{{\mu _0}I}}{{4\pi R}}\left( { - \hat i} \right) = \frac{{ - {\mu _0}I}}{{4\pi R}}\left( {\pi \hat i} \right) \cr & \therefore \overrightarrow B \,{\text{at}}\,{\text{centre}} \cr & \overrightarrow {{B_c}} = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} + \overrightarrow {{B_3}} \cr & = - \frac{{{\mu _0}I}}{{4\pi R}}\left( {\pi \hat i + 2\hat k} \right) \cr} $$

Magnetic field due to segment '1'
$$\eqalign{ & \overrightarrow {{B_1}} = \frac{{{\mu _0}I}}{{4\pi R}}\,\left[ {\sin {{90}^ \circ } + \sin {0^ \circ }} \right]\left( { - \hat k} \right) \cr & = \frac{{ - {\mu _0}I}}{{4\pi R}}\left( {\hat k} \right) = \overrightarrow {{B_3}} \cr} $$
Magnetic field due to segment '2'
$$\eqalign{ & {B_2} = \frac{{{\mu _0}I}}{{4\pi R}}\left( { - \hat i} \right) = \frac{{ - {\mu _0}I}}{{4\pi R}}\left( {\pi \hat i} \right) \cr & \therefore \overrightarrow B \,{\text{at}}\,{\text{centre}} \cr & \overrightarrow {{B_c}} = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} + \overrightarrow {{B_3}} \cr & = - \frac{{{\mu _0}I}}{{4\pi R}}\left( {\pi \hat i + 2\hat k} \right) \cr} $$