Question
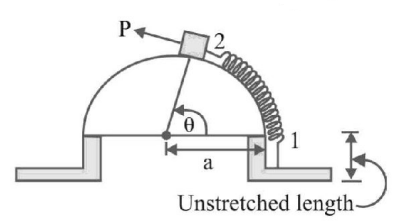
A variable force $$P$$ is maintained tangent to a frictionless cylindrical surface of radius $$a$$ as shown in figure. By slowly varying this force, a block of weight $$W$$ is moved and the spring to which it is stretched from position $$1$$ to position $$2.$$ The work done by the force $$P$$ is
A variable force $$P$$ is maintained tangent to a frictionless cylindrical surface of radius $$a$$ as shown in figure. By slowly varying this force, a block of weight $$W$$ is moved and the spring to which it is stretched from position $$1$$ to position $$2.$$ The work done by the force $$P$$ is
A.
$$W\,a\sin \theta $$
B.
$$\frac{1}{2}k{a^2}{\theta ^2}$$
C.
$$W\,a\sin \theta + k{a^2}{\theta ^2}$$
D.
$$W\,a\sin \theta + \frac{1}{2}k{a^2}{\theta ^2}$$
Answer :
$$W\,a\sin \theta + \frac{1}{2}k{a^2}{\theta ^2}$$
Solution :
$$\eqalign{ & W = mgh + \frac{1}{2}k{x^2} = mg\left( {a\sin \theta } \right) + \frac{1}{2}k{\left( {a\theta } \right)^2} \cr & = W\,a\sin \theta + \frac{1}{2}k{a^2}{\theta ^2}. \cr} $$
$$\eqalign{ & W = mgh + \frac{1}{2}k{x^2} = mg\left( {a\sin \theta } \right) + \frac{1}{2}k{\left( {a\theta } \right)^2} \cr & = W\,a\sin \theta + \frac{1}{2}k{a^2}{\theta ^2}. \cr} $$