Question
A uniform string of length $$20\,m$$ is suspended from a rigid support. A short wave pulse is introduced at its lowest end. It starts moving up the string. The time taken to reach the supports is :
A uniform string of length $$20\,m$$ is suspended from a rigid support. A short wave pulse is introduced at its lowest end. It starts moving up the string. The time taken to reach the supports is :
$$\left( {{\text{take }}g = 10\,m{s^{ - 2}}} \right)$$
A.
$$2\sqrt 2\, s$$
B.
$$\sqrt 2 \,s$$
C.
$$2p\sqrt 2\, s$$
D.
$$2\,s$$
Answer :
$$2\sqrt 2\, s$$
Solution :
We know that velocity in string is given by
$$v = \sqrt {\frac{T}{\mu }} \,\,.....\left( {\text{I}} \right)$$
where, $$\mu = \frac{m}{l} = \frac{{{\text{mass of string}}}}{{{\text{length of string}}}}$$
The tension, $$T = \frac{m}{\ell } \times x \times g\,\,\,.....\left( {{\text{II}}} \right)$$
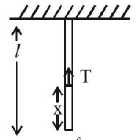
From (I) and (II)
$$\eqalign{ & \frac{{dx}}{{dt}} = \sqrt {gx} \cr & {x^{ - \frac{1}{2}}}dx = \sqrt g dt \cr & \therefore \,\,\int\limits_0^\ell {{x^{ - \frac{1}{2}}}dx - \sqrt g \int\limits_0^\ell {dt} } \cr & 2\sqrt l = \,\sqrt g \times t \cr & \therefore \,\,t = 2\sqrt {\frac{\ell }{g}} \cr & = 2\sqrt {\frac{{20}}{{10}}} \cr & = 2\sqrt 2 \cr} $$
We know that velocity in string is given by
$$v = \sqrt {\frac{T}{\mu }} \,\,.....\left( {\text{I}} \right)$$
where, $$\mu = \frac{m}{l} = \frac{{{\text{mass of string}}}}{{{\text{length of string}}}}$$
The tension, $$T = \frac{m}{\ell } \times x \times g\,\,\,.....\left( {{\text{II}}} \right)$$

From (I) and (II)
$$\eqalign{ & \frac{{dx}}{{dt}} = \sqrt {gx} \cr & {x^{ - \frac{1}{2}}}dx = \sqrt g dt \cr & \therefore \,\,\int\limits_0^\ell {{x^{ - \frac{1}{2}}}dx - \sqrt g \int\limits_0^\ell {dt} } \cr & 2\sqrt l = \,\sqrt g \times t \cr & \therefore \,\,t = 2\sqrt {\frac{\ell }{g}} \cr & = 2\sqrt {\frac{{20}}{{10}}} \cr & = 2\sqrt 2 \cr} $$