Question
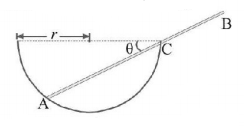
A uniform rod $$AB$$ of length $$3r$$ remains in equilibrium on a hemispherical bowl of radius $$r$$ as shown in figure. Ignoring friction, the inclination of the rod $$\theta $$ with the horizontal is
A uniform rod $$AB$$ of length $$3r$$ remains in equilibrium on a hemispherical bowl of radius $$r$$ as shown in figure. Ignoring friction, the inclination of the rod $$\theta $$ with the horizontal is
A.
$${\cos ^{ - 1}}\left( {\frac{1}{3}} \right)$$
B.
$${\sin ^{ - 1}}\left( {\frac{1}{3}} \right)$$
C.
$${\cos ^{ - 1}}\left( {0.9} \right)$$
D.
$${\sin ^{ - 1}}\left( {0.9} \right)$$
Answer :
$${\cos ^{ - 1}}\left( {0.9} \right)$$
Solution :
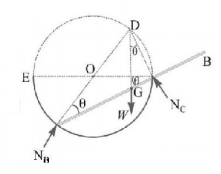
From the geometry
$$\eqalign{ & AD = 2r;AC = 2r\cos \theta \cr & CD = 2r\sin \theta \cr & AG = 1.5r;GC = \left( {2r\cos - 1.5r} \right) \cr & \tan \theta = \frac{{GC}}{{CD}} = \frac{{2r\cos \theta - 1.5r}}{{2r\sin \theta }} \cr} $$
After simplifying, we get, $$\cos \theta = 0.9.$$

From the geometry
$$\eqalign{ & AD = 2r;AC = 2r\cos \theta \cr & CD = 2r\sin \theta \cr & AG = 1.5r;GC = \left( {2r\cos - 1.5r} \right) \cr & \tan \theta = \frac{{GC}}{{CD}} = \frac{{2r\cos \theta - 1.5r}}{{2r\sin \theta }} \cr} $$
After simplifying, we get, $$\cos \theta = 0.9.$$





