Question
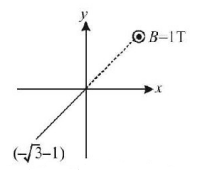
A uniform magnetic field of magnitude $$1\,T$$ exists in region $$y \geqslant 0$$ is along $${\hat k}$$ direction as shown. A particle of charge $$1\,C$$ is projected from point $$\left( { - \sqrt 3 , - 1} \right)$$ towards origin with speed $$1\,m/\sec.$$ If mass of particle is $$1\,kg,$$ then co-ordinates of centre of circle in which particle moves are -
A uniform magnetic field of magnitude $$1\,T$$ exists in region $$y \geqslant 0$$ is along $${\hat k}$$ direction as shown. A particle of charge $$1\,C$$ is projected from point $$\left( { - \sqrt 3 , - 1} \right)$$ towards origin with speed $$1\,m/\sec.$$ If mass of particle is $$1\,kg,$$ then co-ordinates of centre of circle in which particle moves are -
A.
$$\left( {1,\sqrt 3 } \right)$$
B.
$$\left( {1, - \sqrt 3 } \right)$$
C.
$$\left( {\frac{1}{2}, - \frac{{\sqrt 3 }}{2}} \right)$$
D.
$$\left( {\frac{{\sqrt 3 }}{2}, - \frac{1}{2}} \right)$$
Answer :
$$\left( {\frac{1}{2}, - \frac{{\sqrt 3 }}{2}} \right)$$
Solution :

The centre will be at $$C$$ as shown :
Coordinates of the centre are
$$\left( {r\cos {{60}^ \circ }, - r\sin {{60}^ \circ }} \right)$$
where $$r$$ = radius of circle
$$ = \frac{{mv}}{{Bq}} = \frac{{1 \times 1}}{{1 \times 1}} = 1$$
i.e., $$\left( {\frac{1}{2}, - \frac{{\sqrt 3 }}{2}} \right)$$

The centre will be at $$C$$ as shown :
Coordinates of the centre are
$$\left( {r\cos {{60}^ \circ }, - r\sin {{60}^ \circ }} \right)$$
where $$r$$ = radius of circle
$$ = \frac{{mv}}{{Bq}} = \frac{{1 \times 1}}{{1 \times 1}} = 1$$
i.e., $$\left( {\frac{1}{2}, - \frac{{\sqrt 3 }}{2}} \right)$$