Question
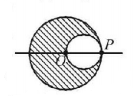
A transparent sphere of radius $$R$$ has a cavity of radius $$\frac{R}{2}$$ as shown in figure. Find the refractive index of the sphere if a parallel beam of light falling on left surface focuses at point $$P.$$
A transparent sphere of radius $$R$$ has a cavity of radius $$\frac{R}{2}$$ as shown in figure. Find the refractive index of the sphere if a parallel beam of light falling on left surface focuses at point $$P.$$
A.
$$\mu = \frac{{3 + \sqrt 5 }}{2}$$
B.
$$\mu = \frac{{3 - \sqrt 5 }}{2}$$
C.
$$\mu = 3 + \sqrt 5 $$
D.
$$\mu = \frac{{1 + \sqrt 5 }}{2}$$
Answer :
$$\mu = \frac{{3 + \sqrt 5 }}{2}$$
Solution :
Let refractive index of glass be $$\mu .$$
Let after first refraction, image distance be $$v$$ then
$$\eqalign{ & \frac{\mu }{v} - \frac{1}{\infty } = \frac{{\mu - 1}}{R} \cr & \Rightarrow v = \frac{{\mu R}}{{\mu - 1}} \cr} $$
Now second refraction will take place.
So distance of first image from $$O$$ is
$$\eqalign{ & {u_1} = \frac{{\mu R}}{{\mu - 1}} - R = \frac{R}{{\mu - 1}}\,\,{\text{and image is formed at }}R \cr & \therefore \frac{1}{R} - \frac{{\mu \left( {\mu - 1} \right)}}{R} = \frac{{2\left( {1 - \mu } \right)}}{R} \cr & \Rightarrow {\mu ^2} - 3\mu + 1 = 0 \cr & {\text{So,}}\,\,\mu = \frac{{3 + \sqrt 5 }}{2} \cr} $$
Let refractive index of glass be $$\mu .$$
Let after first refraction, image distance be $$v$$ then
$$\eqalign{ & \frac{\mu }{v} - \frac{1}{\infty } = \frac{{\mu - 1}}{R} \cr & \Rightarrow v = \frac{{\mu R}}{{\mu - 1}} \cr} $$
Now second refraction will take place.
So distance of first image from $$O$$ is
$$\eqalign{ & {u_1} = \frac{{\mu R}}{{\mu - 1}} - R = \frac{R}{{\mu - 1}}\,\,{\text{and image is formed at }}R \cr & \therefore \frac{1}{R} - \frac{{\mu \left( {\mu - 1} \right)}}{R} = \frac{{2\left( {1 - \mu } \right)}}{R} \cr & \Rightarrow {\mu ^2} - 3\mu + 1 = 0 \cr & {\text{So,}}\,\,\mu = \frac{{3 + \sqrt 5 }}{2} \cr} $$

