Question
A tower stands at the centre of a circular park. $$A$$ and $$B$$ are two points on the boundary of the park such that $$AB (= a)$$ subtends an angle of 60° at the foot of the tower, and the angle of elevation of the top of the tower from $$A$$ or $$B$$ is 30°. The height of the tower is
A.
$$\frac{a}{{\sqrt 3 }}$$
B.
$$a\sqrt 3 $$
C.
$$\frac{2a}{{\sqrt 3 }}$$
D.
$$2a\sqrt 3 $$
Answer :
$$\frac{a}{{\sqrt 3 }}$$
Solution :
In the $$\Delta \,AOB,\angle \,AOB = {60^ \circ },$$ $$\angle \,OBA = \angle \,OAB$$ (since $$OA = OB = AB$$ radius of same circle).
∴ $$\Delta \,AOB$$ is a equilateral triangle. Let the height of tower is $$h$$
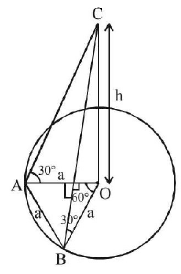
$$m,$$ Given distance between two points $$A$$ & $$B$$ lie on boundary of circular park, subtends an angle of 60° at the foot of the tower is $$AB$$ i.e. $$AB = a. A$$ tower $$OC$$ stands at the centre of a circular park. Angle of elevation of the top of the tower from $$A$$ and $$B$$ is 30°.
In $$\Delta \,OAC$$
$$\eqalign{ & \tan {30^ \circ } = \frac{h}{a} \cr & \Rightarrow \,\,\frac{1}{{\sqrt 3 }} = \frac{h}{a} \cr & \Rightarrow \,\,h = \frac{a}{{\sqrt 3 }} \cr} $$
In the $$\Delta \,AOB,\angle \,AOB = {60^ \circ },$$ $$\angle \,OBA = \angle \,OAB$$ (since $$OA = OB = AB$$ radius of same circle).
∴ $$\Delta \,AOB$$ is a equilateral triangle. Let the height of tower is $$h$$

$$m,$$ Given distance between two points $$A$$ & $$B$$ lie on boundary of circular park, subtends an angle of 60° at the foot of the tower is $$AB$$ i.e. $$AB = a. A$$ tower $$OC$$ stands at the centre of a circular park. Angle of elevation of the top of the tower from $$A$$ and $$B$$ is 30°.
In $$\Delta \,OAC$$
$$\eqalign{ & \tan {30^ \circ } = \frac{h}{a} \cr & \Rightarrow \,\,\frac{1}{{\sqrt 3 }} = \frac{h}{a} \cr & \Rightarrow \,\,h = \frac{a}{{\sqrt 3 }} \cr} $$