Question
A thin uniform rod, pivoted at $$O,$$ is rotating in the horizontal plane with constant angular speed $$\omega ,$$ as shown in the figure. At time $$t=0,$$ a small insect starts from $$O$$ and moves with constant speed $$v,$$ with respect to the rod towards the other end. It reaches the end of the rod at $$t=T$$ and stops. The angular speed of the system remains $$\omega $$ throughout. The magnitude of the torque $$\left( {\left| {\vec \tau } \right|} \right)$$ about $$O,$$ as a function of time is best represented by which plot?
A thin uniform rod, pivoted at $$O,$$ is rotating in the horizontal plane with constant angular speed $$\omega ,$$ as shown in the figure. At time $$t=0,$$ a small insect starts from $$O$$ and moves with constant speed $$v,$$ with respect to the rod towards the other end. It reaches the end of the rod at $$t=T$$ and stops. The angular speed of the system remains $$\omega $$ throughout. The magnitude of the torque $$\left( {\left| {\vec \tau } \right|} \right)$$ about $$O,$$ as a function of time is best represented by which plot?

A.


B.


C.


D.


Answer :


Solution :
We know that $$\left| {\vec \tau } \right| = \left| {\frac{{d\vec L}}{{dt}}} \right|$$ where $$L = I\omega $$
$$\therefore \,\,\tau = \frac{d}{{dt}}\left( {I\omega } \right) = \omega \frac{{dI}}{{dt}}\,.....(i)$$
From the situation it is clear that the moment of inertia for (rod + insect) system is increasing.
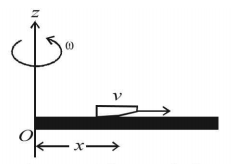
Let at any instant of time $$'t ’,$$ the insect is at a distance $$x$$ from $$O.$$ At this instant, the moment of inertia of the system is
$$\eqalign{ & I = \frac{1}{3}M{L^2} + m{x^2}\,\,.....(ii) \cr & {\text{From }}\,(i)\,\,\& \,\,(ii) \cr & \tau = \omega \frac{d}{{dt}}\left[ {\frac{1}{3}M{L^2} + m{x^2}\,} \right] = \omega m\frac{d}{{dt}}\left( {{x^2}} \right) \cr & = 2\omega mx\frac{{dx}}{{dt}} \cr & = 2\omega mxv\,\,\,\,\,\left[ {\because x = vt} \right] \cr & \therefore \tau \propto t\,\,\,\,\,\left( {{\text{till }}t = T} \right) \cr} $$
When the insect stops moving, $${\vec L}$$ does not change and therefore $$\tau $$ becomes constant.
We know that $$\left| {\vec \tau } \right| = \left| {\frac{{d\vec L}}{{dt}}} \right|$$ where $$L = I\omega $$
$$\therefore \,\,\tau = \frac{d}{{dt}}\left( {I\omega } \right) = \omega \frac{{dI}}{{dt}}\,.....(i)$$
From the situation it is clear that the moment of inertia for (rod + insect) system is increasing.

Let at any instant of time $$'t ’,$$ the insect is at a distance $$x$$ from $$O.$$ At this instant, the moment of inertia of the system is
$$\eqalign{ & I = \frac{1}{3}M{L^2} + m{x^2}\,\,.....(ii) \cr & {\text{From }}\,(i)\,\,\& \,\,(ii) \cr & \tau = \omega \frac{d}{{dt}}\left[ {\frac{1}{3}M{L^2} + m{x^2}\,} \right] = \omega m\frac{d}{{dt}}\left( {{x^2}} \right) \cr & = 2\omega mx\frac{{dx}}{{dt}} \cr & = 2\omega mxv\,\,\,\,\,\left[ {\because x = vt} \right] \cr & \therefore \tau \propto t\,\,\,\,\,\left( {{\text{till }}t = T} \right) \cr} $$
When the insect stops moving, $${\vec L}$$ does not change and therefore $$\tau $$ becomes constant.